The accuracy of the saturation vapour pressure in WUFI
[Scroll down for English version]
Zur Berechnung des Sättigungsdampfdrucks psat für eine gegebene Celsius-Temperatur t benutzt WUFI folgende Formel:
Code: Select all
psat = a*exp(b*t/(c + t)) [Pa]
a = 610.71, b = 22.44, c = 272.44 für t < 0°C
a = 610.78, b = 17.08, c = 234.18 für t >= 0°C
Es können verschiedene Koeffizientensätze verwendet werden, je nachdem ob erhöhte Genauigkeit in einem bestimmten Temperaturbereich oder gleichmäßige Genauigkeit über einen möglichst breiten Temperaturbereich erzielt werden soll. Die hier verwendeten Koeffizientensätze wurden (gerundet) den Aspirationspsychrometer-Tafeln (5. Auflage) des DWD entnommen:
Code: Select all
a = 610.714, b = 22.44294, c = 272.440 für t = -50.9 bis 0.0°C, über Eis
a = 610.780, b = 17.84362, c = 245.425 für t = -50.9 bis 0.0°C, über Wasser
a = 610.780, b = 17.08085, c = 234.175 für t = 0.0 bis 100.9°C, über Wasser

Der absolute Fehler beträgt für positive Temperaturen:
- -0.4 Pa bei 0°C,
- 0 Pa bei 3°C,
- +2.7 Pa bei 23°C,
- 0 Pa bei 34°C,
- -162 Pa bei 91°C
- -127 Pa bei 100 °C.
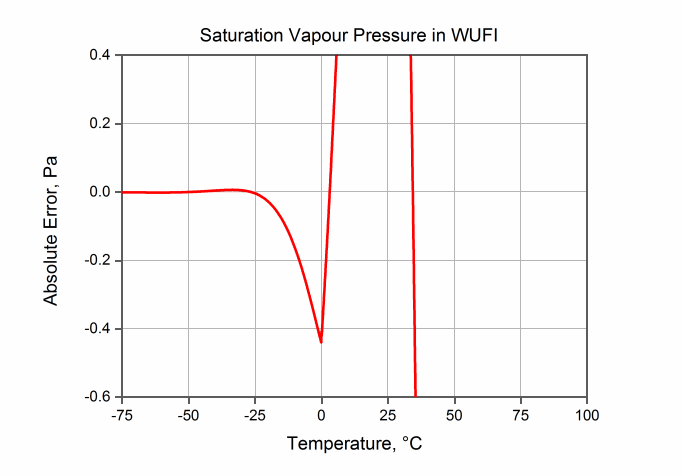
Der absolute Fehler beträgt für negative Temperaturen:
- -0.4 Pa bei 0°C,
- 0 Pa bei -27 °C,
- 0.0063 Pa bei -34°C,
- 0 Pa bei -50°C
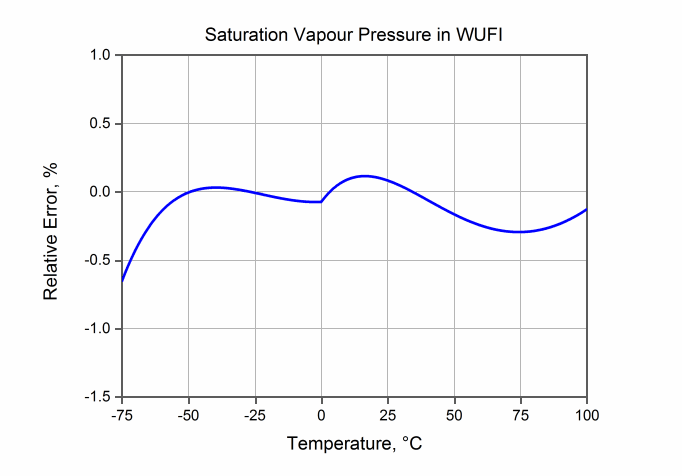
Der relative Fehler beträgt für positive Temperaturen:
- -0.07% bei 0°C,
- 0% bei 3°C,
- +0.12% bei 16°C,
- 0% bei 34°C,
- -0.3% bei 74°C,
- -0.13% bei 100°C
- -0.07% bei 0°C,
- -0.073% bei -2°C,
- 0% bei -27°C,
- 0.03% bei -40°C,
- 0% bei -50°C
WUFI berücksichtigt zwar den Umstand, dass in den feinen Poren von Baustoffen bei Temperaturen unter 0°C ein Teil des Wassers als unterkühlte Flüssigkeit und ein Teil als gefrorenes Eis vorliegt und rechnet Flüssigtransport nur für den nicht gefrorenen Anteil. Es berücksichtigt im Rahmen der bauphysikalischen Vereinfachungen jedoch nicht, dass die beiden Anteile unterschiedliche Sättigungsdampfdrücke haben und setzt pauschal den Sättigungsdampfdruck über Eis an. Der daraus resultierende relative Fehler für den flüssigen Anteil beträgt etwa 20% bei -20°C und 40% bei -50°C [2].
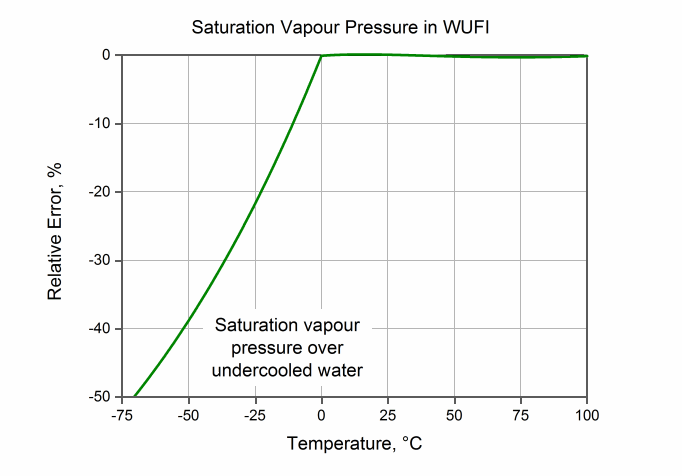
Verdunstungs- und Kondensationsprozesse bei Temperaturen unter 0°C werden daher mit verringerter Genauigkeit berechnet, Umlagerungsprozesse aufgrund unterschiedlicher Dampfdrücke Wasser/Eis werden gar nicht berücksichtigt. WUFI geht davon aus, dass in bauphysikalischem Zusammenhang solch geringe Temperaturen nur kurzzeitig auftreten.
Die obenstehende Diskussion bezieht sich auf die Sättigungsdampfdruck-Formeln, wie sie der Literatur entnommen werden können. Diese beschreiben den Sättigungsdampfdruck von Wasser, wenn es im Gleichgewicht mit seinem Dampf steht, also bei Drücken, die identisch mit dem jeweiligen Sättigungsdampfdruck sind. In der bauphysikalischen Anwendung ist das Wasser jedoch Atmosphärendruck (ca. 1 Bar) ausgesetzt. In dieser Situation ändern sich die Sättigungsdampfdrücke um etwa ein halbes Prozent gegenüber den von den Formeln gegebenen Werten. Diese Korrektur wird von WUFI vernachlässigt und wurde auch in der obigen Diskussion nicht berücksichtigt.
[1] S. Herrmann, H.-J. Kretzschmar, D.P. Gatley: Thermodynamic Properties of Real Moist Air, Dry Air, Steam, Water, and Ice. Final Report - ASHRAE RP-1485
[2] D. Sonntag: Important new Values of the Physical Constants of 1986, Vapour Pressure Formulations based on the ITS-90, and Psychrometer Formulae, Z. Meteorol. 70 (1990) 5, 340-344
**********
WUFI uses the following formula for computing the saturation vapour pressure psat for a given centigrade temperature t:
Code: Select all
psat = a*exp(b*t/(c + t)) [Pa]
a = 610.71, b = 22.44, c = 272.44 für t < 0°C
a = 610.78, b = 17.08, c = 234.18 für t >= 0°C
Different sets of coefficients can be used, depending on whether increased accuracy in a narrow temperature range or uniform accuracy over a wide temperature range is preferred. The (rounded) coefficients used by WUFI have been taken from the aspiration psychrometer tables (5th edition) of the German Meteorological Service DWD:
Code: Select all
a = 610.714, b = 22.44294, c = 272.440 for t = -50.9 bis 0.0°C, over ice
a = 610.780, b = 17.84362, c = 245.425 for t = -50.9 bis 0.0°C, over water
a = 610.780, b = 17.08085, c = 234.175 for t = 0.0 bis 100.9°C, over water
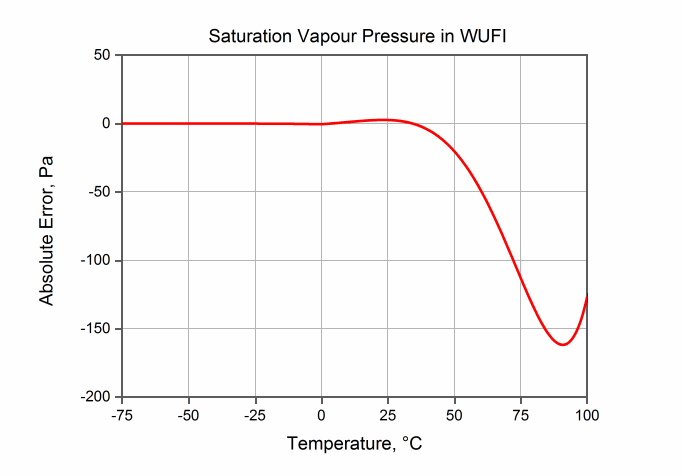
For positive temperatures, the absolute error is:
- -0.4 Pa at 0°C,
- 0 Pa at 3°C,
- +2.7 Pa at 23°C,
- 0 Pa at 34°C,
- -162 Pa at 91°C
- -127 Pa at 100 °C.

For negative temperatures, the absolute error is:
- -0.4 Pa at 0°C,
- 0 Pa at -27 °C,
- 0.0063 Pa at -34°C,
- 0 Pa at -50°C

For positive temperatures, the relative error is:
- -0.07% at 0°C,
- 0% at 3°C,
- +0.12% at 16°C,
- 0% at 34°C,
- -0.3% at 74°C,
- -0.13% at 100°C
- -0.07% at 0°C,
- -0.073% at -2°C,
- 0% at -27°C,
- 0.03% at -40°C,
- 0% at -50°C
WUFI takes into account the fact that at temperatures below 0°C, part of the water in the fine pores of a building material exists as undercooled liquid and part exists as ice, and it considers liquid transport only for the liquid part. However, due to the simplifications which assume typical scenarios encountered in building physics, it does not take into account that the two parts have different vapour pressures, and it uses the saturation vapour pressure over ice for both of them. The relative error for the liquid part incurred by this simplification is about 20% at -20°C and 40% at -50°C [2].

For temperatures below 0°C, evaporation and condensation processes are thus computed with reduced accuracy, and effects like the mass exchange between liquid and frozen phases due to the different vapour pressures are not taken into account at all. WUFI assumes that in simulations of the typical scenarios encountered in building physics these low temperatures only occur for short periods of time.
The discussion presented above only refers to the saturation vapour pressure formulas as found in the literature. These formulas describe the saturation vapour pressure of water when in equilibrium with its own vapour, that is, at the respective saturation pressure. In building materials, however, water is exposed to atmospheric pressure (about 1 bar). Under these circumstances, the saturation vapour pressures differ by about half a percent with respect to the values given by the formulas. This correction is ignored both by WUFI and the above discussion.
[1] S. Herrmann, H.-J. Kretzschmar, D.P. Gatley: Thermodynamic Properties of Real Moist Air, Dry Air, Steam, Water, and Ice. Final Report - ASHRAE RP-1485
[2] D. Sonntag: Important new Values of the Physical Constants of 1986, Vapour Pressure Formulations based on the ITS-90, and Psychrometer Formulae, Z. Meteorol. 70 (1990) 5, 340-344
Keywords: Sättigungsdampfdruck, saturation vapor pressure, saturation vapour pressure
