Luftfeuchte-Tutorial (Deutsch)
Posted: Fri Nov 09, 2018 4:02 am -1100
Luftfeuchte-Tutorial
Die Angaben zur Luftfeuchte beschreiben den Feuchtegehalt der Außen- bzw. Innenluft. In einer hygrothermischen Simulation wird die Feuchte der Umgebungsluft benötigt, um
Es gibt eine Reihe verschiedener Feuchtemaße zur Beschreibung des Feuchtegehalts der Luft. Größtenteils handelt es sich dabei tatsächlich um verschiedene physikalische Größen, nicht nur verschiedene Skalierungen zur Beschreibung derselben Größe. Grad Fahrenheit und Grad Celsius sind beispielweise nur zwei verschiedene Skalierungen derselben physikalischen Größe "Temperatur". Die Umrechnung von Grad Fahrenheit in Grad Celsius ist eine einfache Einheitenumrechnung. Die Umrechnung zwischen verschiedenen Feuchtemaßen hingegen ist eine Umrechnung zwischen verschiedenen physikalischen Größen und muss in der Regel die jeweiligen physikalischen Umstände berücksichtigen.
Die Vielfalt an Feuchtemaßen mag verwirrend erscheinen, aber jede dieser Feuchtegrößen hat ihre eigenen Vorteile in bestimmten Anwendungen. Der Benutzer muss mit diesen Details nicht vertraut sein, um WUFI benutzen zu können. Die folgenden Erläuterungen sollen aber ein tieferes Verständnis hygrischer Prozesse vermitteln oder auch nur bei der Erstellung einer benutzerdefinierten Wetterdatei hilfreich sein.
Luftfeuchte in WUFI
Verschiedene Feuchtegrößen werden benötigt, um verschiedene hygrothermische Vorgänge zu beschreiben:
• In einer hygrothermischen Simulation sind Dampfdruckunterschiede die treibenden Kräfte für Dampfdiffusionstransport, sowohl über die Oberflächen eines Bauteils als auch in seinem Inneren. Diffusionsvorgänge versuchen Dampfdruckunterschiede auszugleichen.
WUFI berechnet aus der Luftfeuchte und dem Feuchtegehalt der Bauteiloberfläche die Dampfdrücke auf beiden Seiten der Oberfläche - in der Luft und im Material. Der Unterschied zwischen beiden bestimmt den Dampfdiffusionsstrom durch die Oberfläche. Der Diffusionsstrom muss dabei die an der Oberfläche haftende Grenzluftschicht überwinden, die als Diffusionswiderstand wirkt. Der Diffusionsstrom durch die Oberfläche ist proportional zum treibenden Dampfdruckunterschied und zum Wasserdampfübergangskoeffizienten, der die Eigenschaften der Grenzluftschicht beschreibt.
Innerhalb des Bauteils verursachen Dampfdruckunterschiede in der Porenluft ebenfalls Dampfdiffusionsströme, die zur Umverteilung von Feuchte im Bauteil führen. Der Diffusionswiderstand der Porenluft wird durch den μ-Wert des Materials beschrieben.
• Sinkt die Oberflächentemperatur des Bauteils unter die Taupunkttemperatur der Umgebungsluft, fällt Tauwasser aus.
• Der Ausgleichsfeuchtegehalt eines porösen Materials in Kontakt mit der Umgebungsluft wird durch die relative Feuchte dieser Luft bestimmt.
Darüber hinaus sind Unterschiede der relativen Feuchte in einem porösen Material die treibenden Kräfte für den kapillaren Transport flüssigen Wassers innerhalb des Materials. Kapillartransport versucht Unterschiede in der relativen Feuchte auszugleichen. Die Stärke des Kapillartransports wird durch die Flüssigtransportkoeffizienten bestimmt.
Wenn ein Temperaturgefälle über dem Bauteil liegt, kann es vorkommen, dass das Dampfdruckgefälle und das Gefälle der relativen Feuchte in entgegengesetzte Richtungen zeigen. In diesem Fall laufen die durch das jeweilige Gefälle in Bewegung gesetzten diffusiven Dampfströme und kapillaren Flüssigkeitsströme ebenfalls gleichzeitig in entgegengesetzte Richtungen. Dies ist ein Beispiel für eine Situation, in der verschiedene Feuchtegrößen maßgeblich die Stärken und Richtungen verschiedener Feuchtetransportmechanismen bestimmen, manchmal sogar gleichzeitig in entgegengesetzte Richtungen.
In Bauteilen stellt sich diese Situation häufig im Winter ein, wenn wegen der niedrigen Außentemperaturen der Dampfdruck in der Innenluft höher ist als der Dampfdruck der Außenluft, während gleichzeitig die relative Feuchte der Außenluft höher ist als die relative Feuchte der Innenluft.
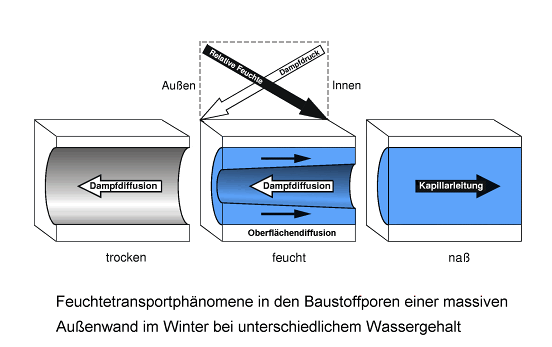
Luftfeuchte-Tutorial
Feuchtemaße
Die Wetterdateiformate, die WUFI lesen kann, benutzen die relative Feuchte als Maß für den Feuchtegehalt der Luft. Wenn Sie Wetterdaten aus anderen Quellen benutzen, können Ihnen aber auch andere Feuchtemaße begegnen. Im Folgenden werden verschiedene gängige Feuchtemaße vorgestellt. Über die bloßen Definitionen hinaus werden auch die jeweiligen Eigenschaften dieser Feuchtemaße erläutert. Die Kenntnis dieser Details ist nicht notwendig, um eine hygrothermische Simulation durchzuführen, sie ist aber hilfreich zum Verständnis feuchtetechnischer Vorgänge.
Die meisten der folgenden Feuchtemaße hängen nicht nur von der Menge der in der Luft enthaltenen Feuchtigkeit ab, sondern auch von der Temperatur und/oder dem Druck der Luft. Sie ändern sich also nicht nur, wenn Wassermoleküle der Luft hinzugefügt oder aus der Luft entfernt werden, sondern auch wenn sich die Temperatur oder der Druck ändern. Dies ist keine Unzulänglichkeit dieser Feuchtemaße, es ist vielmehr zweckmäßig für die Beschreibung der jeweiligen Eigenschaften feuchter Luft. Sie sollten sich dieser Eigenschaften der verschiedenen Feuchtemaße aber bewusst sein, um Fehlinterpretationen zu vermeiden.
Insbesondere hängt die Wahl eines geeigneten Feuchtemaßes davon ab, ob ausschließlich eine quantitative Aussage über die vorhandene Feuchtemenge beabsichtigt ist, oder auch eine Aussage über eine der Auswirkungen des Feuchtegehalts.
In hygrothermischen Gebäudesimulationen ist der Druck in der Regel der Atmosphärendruck, dessen Schwankungen üblichweise nur vernachlässigbare Auswirkungen auf das Simulationsergebnis haben. Die Druckabhängigkeit kann aber beispielsweise in Druckluftsystemen wichtig sein.
• Wasserdampfpartialdruck
Der Wasserdampfpartialdruck, kurz Wasserdampfdruck oder Dampfdruck, ist der Druck, den der in der Luft enthaltene Wasserdampf zum Gesamtdruck der Luft beiträgt (Daltonsches Gesetz).
Trockene Luft und Wasserdampf können in guter Näherung als ideale Gase behandelt werden, die sich auch in der Mischung "feuchte Luft" gegenseitig nicht beeinflussen. Daher gilt insbesondere für den im betrachteten Luftpaket enthaltenen Wasserdampf das ideale Gasgesetz
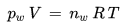
pw [Pa] : Wasserdampfpartialdruck im Luftpaket
V [m3] : Volumen des Luftpakets
nw [mol] : Molzahl der Wasserdampfmoleküle im Luftpaket
R [J/(mol K)] : universelle Gaskonstante, 8.314 J/(mol K)
T [K] : absolute Temperatur des Luftpakets
Auflösen der Gleichung nach dem Partialdruck pw liefert
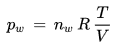
Bei festgehaltenem Verhältnis T/V von Volumen V und Temperatur T eines gegebenen Luftpakets nimmt der Wasserdampfdruck pw also zu, wenn Wassermoleküle der Luft hinzugefügt werden, weil unter diesen Bedingungen der Druck eines Gases proportional zur Anzahl seiner Moleküle ist (Avogadros Gesetz). Der Wasserdampfdruck ist unter diesen Bedingungen ein direktes Maß für die Anzahl der im Luftpaket enthaltenen Wassermoleküle.
Der Wasserdampfdruck kann sich im Allgemeinen aber auch ändern, ohne dass Wassermoleküle hinzugefügt oder entfernt werden. Der Wasserdampfdruck in einem gegebenen Luftpaket nimmt beispielsweise proportional zur Temperatur T zu, wenn T bei festgehaltenem Volumen V und festgehaltener Molekülzahl nw erhöht wird (Gesetz von Amontons, die Moleküle bewegen sich schneller), er nimmt proportional zu 1/V zu, wenn das Volumen V bei festgehaltener Temperatur T und festgehaltener Molekülzahl nw komprimiert wird (Gesetz von Boyle-Mariotte, aufgrund ihrer höheren Dichte treffen die Moleküle häufiger auf die Behälterwand). Der letztere Fall tritt beispielsweise in Luftkompressoren auf: Wenn die Luft so stark komprimiert wird, dass der erhöhte Dampfdruck des enthaltenen Wasserdampfs den Sättigungsdampfdruck bei der aktuellen Temperatur übersteigt, fällt Kondensat aus. Wenn zwei oder alle drei Variablen auf der rechten Seite variieren, beschreibt das ideale Gasgesetz die zugehörige Variation des Wasserdampfdrucks.
In hygrothermischen Simulationen sind üblicherweise weder T noch V festgehalten. Die Temperatur stellt sich nach Maßgabe der Randbedingungen und der hygrothermischen Prozesse ein. Das Volumen eines gegebenen Luftpakets kann sich frei zusammenziehen oder ausdehnen, wenn Temperatur oder Gesamtdruck sich ändern.
Für die aus trockener Luft und Wasserdampf bestehende Mischung "feuchte Luft" gilt ebenfalls das ideale Gasgesetz
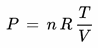
P [Pa] : Gesamtdruck des Luftpakets
(= Summe aus den Partialdrücken ptr der trockenen Luft und pw des enthaltenen Wasserdampfs)
n [mol] : Gesamtmolzahl im Luftpaket
(= Summe aus den Molzahlen ntr der trockenen Luft und nw des enthaltenen Wasserdampfs)
Division des idealen Gasgesetzes für den Wasserdampf durch das ideale Gasgesetz für die feuchte Luft liefert den folgenden Zusammenhang zwischen dem Wasserdampfpartialdruck pw und dem Gesamtdruck P:
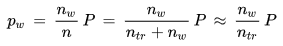
Der Partialdruck des Wasserdampfs ergibt sich also, indem der Gesamtdruck P des Gemisches mit dem Stoffmengenanteil nw/n des Wasserdampfs multipliziert wird. Dies ist das Daltonsche Gesetz.
Die im letzten Schritt vorgenommene Näherung ist in normaler atmosphärischer Luft gerechtfertigt, da in ihr die Molzahl nw des Wasserdampfs gering ist im Vergleich zur Molzahl ntr der trockenen Luft (in gesättigter Luft bei 20 °C kommt ein Wassermolekül auf 43 Luftmoleküle). In diesem Fall ist - bei festgehaltener Molzahl ntr der trockenen Luft und festgehaltenem Gesamtdruck P - der Partialdruck ein direktes Maß für die im Luftpaket enthaltene Molzahl der Wasserdampfmoleküle.
Wie die Formel zeigt, kann sich der Zahlenwert des Partialdrucks auch bei konstanter Anzahl von Wassermolekülen ändern, wenn sich der Gesamtdruck ändert. Er bleibt bei meteorologisch oder technisch vorgegebenem Gesamtdruck jedoch unbeeinflusst von eventuellen Änderungen der Temperatur oder des Volumens des betrachteten Luftpakets.
Die meteorologisch bedingten Änderungen des Gesamtdrucks gehen nur langsam vor sich, ihr Einfluss wird in vielen Messreihen vernachlässigbar sein, muss aber beim Vergleich von Feuchtemessungen verschiedener Zeitperioden oder Standorte unter Umständen berücksichtigt werden.
Der Wasserdampfpartialdruck kann den Sättigungsdampfdruck psat nicht übersteigen, sofern sich Oberflächen in der Nähe befinden, auf denen Feuchte kondensieren kann. Solche Oberflächen sind praktisch immer vorhanden, denn es kann sich beispielsweise um Wandoberflächen handeln (Tauwasserausfall), aber auch um schwebende Staubteilchen, die als Kondensationskerne dienen (Nebelbildung).
Der Sättigungsdampfdruck ist stark temperaturabhängig. Bei 0 °C beträgt er beispielsweise 611 Pa, bei 20 °C beträgt er 2339 Pa. Eine Formel zur Berechnung des Sättigungsdampfdrucks wird weiter unten angegeben.
Anmerkung: Die eben beschriebene Obergrenze für den Feuchtegehalt wird oft so ausgedrückt, dass die Luft bei gegebener Temperatur nur eine bestimmte maximale Feuchtemenge aufnehmen könne. Diese Ausdrucksweise ist irreführend, da sie nahelegt, die Maximalmenge sei durch die Eigenschaften der Luft bestimmt - so als ob die Luft ein Schwamm sei, der die Feuchtigkeit aufsaugt und bei einer bestimmten Menge seine Aufnahmekapazität erschöpft hat. Dies trifft nicht zu - wie oben erwähnt wechselwirken Luft und Wasserdampf so gut wie gar nicht. Der maximal mögliche Wasserdampf-Partialdruck ist beispielsweise in einer reinen Edelgasatmosphäre oder sogar im Vakuum derselbe wie in Luft. Außerdem zeigt die Erfahrung, dass andere flüchtige Flüssigkeiten (etwa Benzin oder Alkohol) auch in "feuchtegesättigte Luft" hinein verdunsten können, so dass offenbar die Vorstellung einer erschöpften Aufnahmekapazität nicht richtig sein kann.
Der maximal mögliche Partialdruck wird vielmehr durch die Eigenschaften des Wasserdampfs selbst bestimmt, nämlich die beim Sättigungs-Partialdruck beginnende Kondensationsfähigkeit. Kurzzeitige Übersättigung kann oft vorkommen, der Partialdruck reduziert sich dann aber infolge Kondensation schnell wieder auf den Sättigungswert (ein Beispiel folgt im nächsten Abschnitt). In besonders reiner Luft ohne nahe Kondensationsflächen (z.B. in der Atmosphäre in großer Höhe) kann der Sättigungsdampfdruck längere Zeit um das Zwei- bis Dreifache überschritten werden.
Fazit: Dampfdruckunterschiede sind die treibenden Kräfte für die Dampfdiffusion, sie bestimmen also die Dampfdiffusion innerhalb des Bauteils und über die Bauteilgrenzen. Die Dampfmenge in der Luft ist durch den Sättigungsdampfdruck beschränkt. Vergleich des aktuellen Dampfdrucks mit dem der aktuellen Temperatur entsprechenden Sättigungsdampfdruck erlaubt die Möglichkeit (und gegebenenfalls die Rate) von Kondensation zu bestimmen.
• Relative Feuchte
Die relative Feuchte ist definiert als das Verhältnis des aktuellen Wasserdampfpartialdruckes in der Luft zu dem der aktuellen Lufttemperatur entsprechenden Sättigungsdampfdruck. Sie wird als Prozentsatz (z.B. 78 %) oder Verhältniszahl (z.B. 0.78) ausgedrückt.
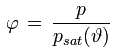
φ [%] oder [-] : relative Feuchte
p [Pa] : Wasserdampfpartialdruck
psat(ϑ) [Pa] : Wasserdampfsättigungsdruck bei der Temperatur ϑ
Die Abhängigkeit der relativen Feuchte von der Anzahl der in der Luft vorhandenen Wassermoleküle unter gegebenen Bedingungen ist der Definition entsprechend dieselbe wie die Abhängigkeit des Wasserdampfpartialdrucks p unter diesen Bedingungen (siehe z.B. die oben beschriebenen Einflüsse von Temperatur, Volumen oder Gesamtdruck). Zusätzlich liegt jedoch eine starke Temperaturabhängigkeit vor: Wenn die Temperatur zunimmt, nimmt auch der temperaturabhängige Sättigungsdampfdruck psat zu, und auch in Situationen, in denen der Wasserdampfdruck p dabei konstant bleibt, nimmt die relative Feuchte ab.
Wenn die relative Feuchte der Luft 100 % erreicht, ist die Luft mit Feuchtigkeit gesättigt und der Partialdruck ist gleich dem Sättigungsdampfdruck. Weitere Feuchtezufuhr führt zur Kondensation der überschüssigen Feuchte (siehe oben). Beachten Sie, dass eine feuchte Oberfläche unter Umständen auch dann Feuchte in die Außenluft abgeben kann, wenn diese bereits gesättigt ist: Sofern die Temperatur der Oberfläche über der Lufttemperatur liegt, kann sie einen höheren Partialdruck aufweisen, so daß aufgrund des Dampfdruckunterschieds ein von der Oberfläche fort gerichteter Diffusionsstrom einsetzt. Dies führt zur Übersättigung der oberflächennahen Luft und Kondensatausfall in der Luft (z.B. in Form von sichtbaren Dampfschwaden).
Der in den Poren eines porösen hygroskopischen Materials adsorbierte Ausgleichswassergehalt hängt ab vom Verhältnis der Adsorptionsrate (wird bestimmt vom Wasserdampfpartialdruck p in der Porenluft) zur Verdunstungsrate (wird im Wesentlichen bestimmt durch den Sättigungsdampfdruck psat über den adsorbierten Wasseroberflächen). Er hängt daher von der relativen Feuchte φ der Porenluft und damit letztlich von der relativen Feuchte der Umgebungsluft ab, der das Material ausgesetzt ist (statt beispielsweise der absoluten Feuchte der Umgebungsluft). Die Feuchtespeicherfunktion beschreibt den Ausgleichswassergehalt daher als Funktion der relativen Feuchte.
Die meisten Instrumente zur Messung des Feuchtegehalts der Luft benutzen feuchtegehaltsabhängige Eigenschaften geeigneter Materialien (z.B. Längenänderungen von Fasern, Änderungen der elektrischen Eigenschaften von Polymeren, usw). Da der Feuchtegehalt dieser Materialien von der relativen Feuchte der Umgebungsluft bestimmt wird, ist das von diesen Instrumenten gemessene Feuchtemaß die relative Feuchte der Luft.
Der in der Definition der relativen Feuchte verwendete Sättigungsdampfdruck psat setzt chemisch reines Wasser und eine flache Wasseroberfläche voraus. Wenn sich gelöste Stoffe (z.B. Salze) im Wasser befinden, oder wenn die Oberfläche konkav gekrümmt ist (z.B. in kleinen Poren), ist der tatsächliche Sättigungsdampfdruck verringert und Sättigungsgleichgewicht tritt schon bei weniger als 100 % relativer Feuchte auf (denn auch unter diesen Umständen wird definitionsgemäß der Sättigungsdampfdruck über reinem Wasser und einer ebenen Wasseroberfläche als Referenz verwendet).
So beträgt beispielsweise der Gleichgewichtsdampfdruck über einer gesättigten Kochsalzlösung bei 20 °C nicht 2339 Pa (wie über reinem Wasser), sondern wegen der geringeren Konzentration der Wassermoleküle in der Lösung nur 1765 Pa, so dass sich in der Luft über der Salzlösung eine relative Feuchte von 1765 Pa / 2339 Pa = 75.4 % einstellt. Eine gesättigte Kochsalzlösung kann daher zur Einstellung und Konstanthaltung dieser relativen Feuchte benutzt werden, was beispielsweise die gezielte Konditionierung einer Materialprobe zur Bestimmung der Feuchtespeicherfunktion bei dieser Feuchte ermöglicht.
Liegt flüssiges Wasser im Porenraum eines porösen Materials vor, dann sind die Wasseroberflächen in den Poren aufgrund der Kapillarkräfte konkav gekrümmte "Menisken". Wegen der stärkeren Bindung der Wassermoleküle in den gekrümmten Wasseroberflächen ist der Gleichgewichtsdampfdruck gegenüber dem Gleichgewichtsdampfdruck über einer ebenen Wasseroberfläche vermindert.
Die relative Feuchte der Porenluft, die im hygrischen Gleichgewicht mit den gekrümmten Menisken der Wasseroberflächen steht, beträgt also weniger als 100 %, wobei der genaue Zahlenwert von der Krümmung der Menisken abhängt.
Andererseits übt ein Meniskus Zugkräfte auf das Porenwasser aus und erzeugt so einen (negativen) Kapillardruck im Wasser, wobei der genaue Zahlenwert ebenfalls von der Krümmung der Menisken abhängt.
Mit anderen Worten: Im hygrischen Gleichgewicht existiert ein mathematischer Zusammenhang zwischen der relativen Feuchte der Porenluft und dem Kapillardruck im Wasser. Da Kapillardruckunterschiede den kapillaren Flüssigtransport antreiben, lässt sich mit gleichem Recht auch sagen, dass Unterschiede in relativer Feuchte den kapillaren Flüssigtransport antreiben. In der Tat benutzen WUFIs Transportgleichungen die relative Feuchte als treibendes Potential, weil sie gegenüber dem Wassergehalt als treibendem Potential Vorteile hat.
Die Kelvin-Gleichung beschreibt den funktionellen Zusammenhang zwischen der relativen Feuchte der Porenluft und dem Kapillardruck im Porenwasser:
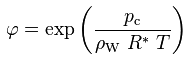
φ [-] : relative Feuchte der Porenluft
pc [Pa] : Kapillardruck im Porenwasser, bezogen auf den Umgebungsdruck
ρW [kg/m3] : Dichte des Wassers, 1000 kg m-3
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
T [K] : absolute Temperatur
Die folgende Tabelle zeigt einige Beispiele für den Zusammenhang zwischen dem Krümmungsradius der Menisken, dem durch die Meniskenkrümmung erzeugten Kapillardruck im Porenwasser und der relativen Feuchte der Porenluft, die sich im Gleichgewicht über den gekrümmten Menisken einstellt:

Der Zusammenhang zwischen der Meniskenkrümmung (Krümmungsradius r) und dem Kapillardruck pc ist gegeben durch pc = 2 σ / r mit der Oberflächenspannung σ (0.072 N/m bei 25°C). Der Zusammenhang zwischen dem Kapillardruck und der relativen Feuchte ist gegeben durch die Kelvin-Gleichung.
In einer Kapillare mit dem Radius rc nimmt ein Meniskus den Krümmungsradius r = rc / cos(γ) an. γ ist der von der Benetzbarkeit des Porenmaterials abhängige Kontaktwinkel zwischen dem Meniskusrand und der Porenwand. Für gut benetzbare Materialien ist cos(γ) ≈ 1 und der in der Tabelle aufgeführte Meniskenradius kann näherungsweise gleich dem Radius der größten gefüllten Poren gesetzt werden.
Wie der Tabelle zu entnehmen ist, beträgt beispielsweise die Gleichgewichtsfeuchte über teilweise gefüllten Poren mit dem Radius 0.005 µm etwa 80 %. Bei einer relativen Porenluftfeuchte von 80 % füllen sich daher die Poren mit Radien unter 0.005 µm infolge "Kapillarkondensation", weil in ihnen bereits bei 80 % relativer Feuchte Übersättigung vorliegt. In den kleinen Poren kann daher bereits bei relativen Feuchten von 80..90 % (je nach Porenradienverteilung des betrachteten Materials) flüssiges Wasser kondensieren, was zu einem starken Anstieg der Ausgleichswassergehalte bei diesen Luftfeuchteniveaus führt, einem typischen Charakteristikum der Feuchtespeicherfunktionen gängiger Materialien.
• Wasserdampfkonzentration, absolute Feuchte
Die Wasserdampfkonzentration (auch: absolute Feuchte) ist das Verhältnis der Masse des in einem Paket feuchter Luft enthaltenen Wasserdampfes zum Volumen des Pakets:
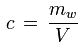
c [g/m3] : Wasserdampfkonzentration, absolute Feuchte
mw [kg] : Masse des im Luftpaket enthaltenen Wasserdampfs
V [m3] : Volumen des Luftpakets
Der Zusammenhang zwischen der Wasserdampfkonzentration und dem Wasserdampfpartialdruck ist durch das ideale Gasgesetz gegeben:
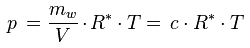
p [Pa] : Wasserdampfpartialdruck
c [kg/m3] : Wasserdampfkonzentration
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
T [K] : absolute Temperatur
nach c aufgelöst also:
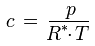
Die Abhängigkeit der Wasserdampfkonzentration von der Anzahl der in der Luft vorhandenen Wassermoleküle unter gegebenen Bedingungen ist demnach dieselbe wie die Abhängigkeit des Wasserdampfpartialdrucks p unter diesen Bedingungen (siehe z.B. die oben beschriebenen Einflüsse von Temperatur, Volumen oder Gesamtdruck). Es liegt jedoch eine zusätzliche Temperaturabhängigkeit vor: Wenn die Temperatur zunimmt (bei festgehaltenem Gesamtdruck, wie es in hygrothermischen Simulationen üblicherweise der Fall ist), nimmt die Wasserdampfkonzentration in einem gegebenen Luftpaket ab, weil sich dann das Volumen des Pakets ausdehnt und die Masse des in der Luft enthaltenen Wassers sich auf ein größeres Volumen V verteilt.
Die Wasserdampfkonzentration kann gemessen werden, indem man mit einem starken Absorber alles Wasser in einem bekannten Luftvolumen absorbiert und durch Wägung die absorbierte Wassermenge bestimmt.
Typische Werte sind 4.8 g/m3 bei 0 °C und Sättigung, und 17.3 g/m3 bei 20 °C und Sättigung.
• Mischungsverhältnis, Wassergehalt, Feuchtegrad
Das Mischungsverhältnis (auch: Wassergehalt, Feuchtegrad) eines gegebenen Pakets feuchter Luft ist das Verhältnis der in diesem Paket enthaltenen Masse des Wasserdampfes zur Masse der trockenen Luft:
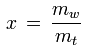
x [kg/kg] : Mischungsverhältnis
mw [kg] : Masse des im Paket enthaltenen Wasserdampfs
mt [kg] : Masse der im Paket enthaltenen trockenen Luft
Das Mischungsverhältnis ändert sich nur dann, wenn Wassermoleküle der Luft hinzugefügt oder entnommen werden. Wenn die Temperatur des Luftpakets zunimmt, vergrößert sich dessen Volumen, aber das Verhältnis zwischen der Anzahl der Wassermoleküle und der Anzahl der Luftmoleküle im Paket bleibt unverändert, also bleibt auch das Verhältnis ihrer Massen unverändert. Dasselbe gilt für Volumenänderungen, die durch Druckänderungen verursacht werden.
Wird beispielsweise feuchte Luft durch ein Rohrsystem mit abschnittsweise unterschiedlichen Temperaturen und Drücken gepumpt, bleibt das Mischungsverhältnis auf dem ganzen Weg dasselbe, solange keine Kondensation oder Verdunstung auftritt.
Der Zusammenhang zwischen dem Mischungsverhältnis und dem Wasserdampfpartialdruck ist gegeben durch die Formel
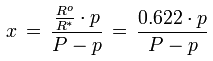
x [kg/kg] : Mischungsverhältnis
Ro [J/(kg K)] : Gaskonstante für trockene Luft, 287.1 J/(kg K)
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
p [Pa] : Wasserdampfpartialdruck
P [Pa] : Luftdruck
• Spezifische Feuchte
Die spezifische Feuchte eines gegebenen Pakets feuchter Luft ist das Verhältnis der in diesem Paket enthaltenen Masse des Wasserdampfes zur Masse der feuchten Luft (d.h. zur Summe der Massen von Wasserdampf und trockener Luft):
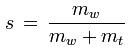
s [kg/kg] : spezifische Feuchte
mw [kg] : Masse des im Paket enthaltenen Wasserdampfs
mt [kg] : Masse der im Paket enthaltenen trockenen Luft
Ebenso wie beim Mischungsverhältnis ändert sich die spezifische Feuchte nur dann, wenn Wassermoleküle der Luft hinzugefügt oder entnommen werden. Besteht die feuchte Luft fast nur aus Wasserdampf und wenig Luft, nimmt die spezifische Feuchte Werte nahe 1 an, während das Mischungsverhältnis sich dem Wert Unendlich nähert.
Der Zusammenhang zwischen der spezifischen Feuchte und dem Wasserdampfpartialdruck ist durch die folgende Formel gegeben:
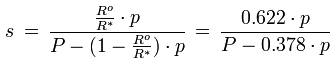
s [kg/kg] : spezifische Feuchte
Ro [J/(kg K)] : Gaskonstante für trockene Luft, 287.1 J/(kg K)
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
p [Pa] : Wasserdampfpartialdruck
P [Pa] : Luftdruck
• Taupunkttemperatur
Die Taupunkttemperatur feuchter Luft ist jene Temperatur, auf welche ein Paket feuchter Luft bei konstantem Gesamtdruck und konstanter Anzahl enthaltener Wassermoleküle gekühlt werden müsste, damit der enthaltene Wasserdampf Sättigung erreicht und zu kondensieren beginnt.
Der größte bei einer gegebenen Temperatur ϑ auftretende Wasserdampfdruck ist, wie oben erwähnt, der Sättigungsdampfdruck psat(ϑ).
Die Taupunkttemperatur ϑTau von Luft, die Wasserdampf mit dem Dampfdruck p enthält, ist die fiktive Temperatur, für die gilt
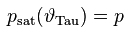
psat [Pa] : Sättigungsdampfdruck
ϑTau [°C] : Taupunkttemperatur
p [Pa] : aktueller Wasserdampfpartialdruck
Die Taupunkttemperatur ist also ein Maß für den Wasserdampfpartialdruck. Sie drückt den Wasserdampfpartialdruck lediglich durch jene Temperatur aus, die man in einer Sättigungsdampfdruckformel einsetzen muss, damit die Formel den betreffenden Wasserdampfpartialdruck liefert. Die obigen Bemerkungen zur Temperatur- und Druckabhängigkeit des Wasserdampfpartialdrucks treffen daher auch auf die Taupunkttemperatur zu.
Bei einem Wasserdampfpartialdruck von 611 Pa beträgt die Taupunkttemperatur 0 °C, bei 2339 Pa beträgt sie 20 °C .
Die Taupunkttemperatur ist ein geeignetes Feuchtemaß zur Beurteilung, wann Kondensation auftreten kann.
Die Taupunkttemperatur der Luft kann direkt mit einem gekühlten Taupunktspiegel gemessen werden.
• Feuchtkugeltemperatur
Die Feuchtkugeltemperatur ist die Temperatur, die ein mit einem befeuchteten Stoffüberzug versehenes Thermometer anzeigt. Sie liegt aufgrund der Verdunstungskühlung unter der von einem trockenen Thermometer angezeigten Lufttemperatur. Das Ausmaß der Kühlung ist abhängig von der Verdunstungsrate, welche in feuchter Luft kleiner ist als in trockener Luft. Die Umrechnung in andere Feuchtemaße geschieht mittels Psychrometertabellen oder empirischer Psychrometerformeln.
Die Feuchtkugeltemperatur der Luft kann direkt mit einem entsprechend ausgestatteten Thermometer gemessen werden.
Zusammenfassung
Die einzigen geläufigen Feuchtemaße, die sich nur dann ändern, wenn dem betrachteten Luftpaket Wassermoleküle hinzugefügt oder entzogen werden, sind das Mischungsverhältnis x und die spezifische Feuchte s. Diese Feuchtemaße beschreiben also den Feuchtegehalt im engeren Sinn.
Die anderen Feuchtemaße ändern sich zusätzlich bei Änderungen von Druck, Volumen oder Temperatur. Dies kann für den beabsichtigten Zweck erwünscht oder unerwünscht sein. Die folgende Tabelle gibt einen Überblick darüber, von welchen zusätzlichen Variablen die einzelnen Feuchtemaße beeinflusst werden (konstante Anzahl von Molekülen trockener Luft im Luftpaket stets vorausgesetzt).
Dabei wird der in der Hygrothermik häufig vorkommende Fall vorausgesetzt, dass der Gesamtdruck P vorgegeben ist, so dass die Formeln soweit möglich unter Verwendung von P formuliert sind. Falls stattdessen Temperatur und Volumen vorgegeben sind, bietet es sich an, die Formeln unter Verwendung des idealen Gasgesetzes für den Gesamtdruck entsprechend umzuformulieren.
Der Sättigungsdampfdruck ist der Wasserdampfpartialdruck, der sich bei einer gegebenen Temperatur im Gleichgewicht über einer flachen Wasseroberfläche einstellt. Es existiert eine Vielzahl verschieden aufwändiger und verschieden genauer empirischer Formeln zur Berechnung des Sättigungsdampfdrucks. Einen günstigen Kompromiss zwischen Aufwand und Genauigkeit bieten Formeln vom Magnus-Typ. Sie können außerdem explizit nach der Taupunkttemperatur aufgelöst werden, die einem gegebenen Wasserdampfpartialdruck entspricht. Ein Beispiel für eine Magnus-Formel und ihre Inverse ist
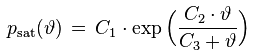
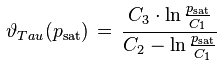
psat [Pa] : Sättigungsdampfdruck
ϑ [°C] : Temperatur
ϑTau [°C] : Taupunkttemperatur
mit dem folgenden Koeffizientensatz [1]:

Über einer konkav gekrümmten Wasseroberfläche (z.B. dem Meniskus in einer teilweise gefüllten Materialpore) ist der Sättigungsdampfdruck kleiner als über einer flachen Oberfläche, siehe Kelvin-Gleichung. Die sehr geringe Abhängigkeit des Sättigungsdampfdrucks vom Luftdruck wird üblicherweise vernachlässigt.
Literatur:
[1] Deutscher Wetterdienst: Aspirations-Psychrometer-Tafeln.
5. Auflage, Vieweg
Update: 2019-05-02, TS
Update: 2020-09-02, TS
Die Angaben zur Luftfeuchte beschreiben den Feuchtegehalt der Außen- bzw. Innenluft. In einer hygrothermischen Simulation wird die Feuchte der Umgebungsluft benötigt, um
- die Stärke des Dampfdiffusions-Austauschs zwischen der Bauteiloberfläche und der Umgebungsluft und
- den Ausgleichsfeuchtegehalt eines Materials im Kontakt mit der Luft
Es gibt eine Reihe verschiedener Feuchtemaße zur Beschreibung des Feuchtegehalts der Luft. Größtenteils handelt es sich dabei tatsächlich um verschiedene physikalische Größen, nicht nur verschiedene Skalierungen zur Beschreibung derselben Größe. Grad Fahrenheit und Grad Celsius sind beispielweise nur zwei verschiedene Skalierungen derselben physikalischen Größe "Temperatur". Die Umrechnung von Grad Fahrenheit in Grad Celsius ist eine einfache Einheitenumrechnung. Die Umrechnung zwischen verschiedenen Feuchtemaßen hingegen ist eine Umrechnung zwischen verschiedenen physikalischen Größen und muss in der Regel die jeweiligen physikalischen Umstände berücksichtigen.
Die Vielfalt an Feuchtemaßen mag verwirrend erscheinen, aber jede dieser Feuchtegrößen hat ihre eigenen Vorteile in bestimmten Anwendungen. Der Benutzer muss mit diesen Details nicht vertraut sein, um WUFI benutzen zu können. Die folgenden Erläuterungen sollen aber ein tieferes Verständnis hygrischer Prozesse vermitteln oder auch nur bei der Erstellung einer benutzerdefinierten Wetterdatei hilfreich sein.
Luftfeuchte in WUFI
Verschiedene Feuchtegrößen werden benötigt, um verschiedene hygrothermische Vorgänge zu beschreiben:
• In einer hygrothermischen Simulation sind Dampfdruckunterschiede die treibenden Kräfte für Dampfdiffusionstransport, sowohl über die Oberflächen eines Bauteils als auch in seinem Inneren. Diffusionsvorgänge versuchen Dampfdruckunterschiede auszugleichen.
WUFI berechnet aus der Luftfeuchte und dem Feuchtegehalt der Bauteiloberfläche die Dampfdrücke auf beiden Seiten der Oberfläche - in der Luft und im Material. Der Unterschied zwischen beiden bestimmt den Dampfdiffusionsstrom durch die Oberfläche. Der Diffusionsstrom muss dabei die an der Oberfläche haftende Grenzluftschicht überwinden, die als Diffusionswiderstand wirkt. Der Diffusionsstrom durch die Oberfläche ist proportional zum treibenden Dampfdruckunterschied und zum Wasserdampfübergangskoeffizienten, der die Eigenschaften der Grenzluftschicht beschreibt.
Innerhalb des Bauteils verursachen Dampfdruckunterschiede in der Porenluft ebenfalls Dampfdiffusionsströme, die zur Umverteilung von Feuchte im Bauteil führen. Der Diffusionswiderstand der Porenluft wird durch den μ-Wert des Materials beschrieben.
• Sinkt die Oberflächentemperatur des Bauteils unter die Taupunkttemperatur der Umgebungsluft, fällt Tauwasser aus.
• Der Ausgleichsfeuchtegehalt eines porösen Materials in Kontakt mit der Umgebungsluft wird durch die relative Feuchte dieser Luft bestimmt.
Darüber hinaus sind Unterschiede der relativen Feuchte in einem porösen Material die treibenden Kräfte für den kapillaren Transport flüssigen Wassers innerhalb des Materials. Kapillartransport versucht Unterschiede in der relativen Feuchte auszugleichen. Die Stärke des Kapillartransports wird durch die Flüssigtransportkoeffizienten bestimmt.
Wenn ein Temperaturgefälle über dem Bauteil liegt, kann es vorkommen, dass das Dampfdruckgefälle und das Gefälle der relativen Feuchte in entgegengesetzte Richtungen zeigen. In diesem Fall laufen die durch das jeweilige Gefälle in Bewegung gesetzten diffusiven Dampfströme und kapillaren Flüssigkeitsströme ebenfalls gleichzeitig in entgegengesetzte Richtungen. Dies ist ein Beispiel für eine Situation, in der verschiedene Feuchtegrößen maßgeblich die Stärken und Richtungen verschiedener Feuchtetransportmechanismen bestimmen, manchmal sogar gleichzeitig in entgegengesetzte Richtungen.
In Bauteilen stellt sich diese Situation häufig im Winter ein, wenn wegen der niedrigen Außentemperaturen der Dampfdruck in der Innenluft höher ist als der Dampfdruck der Außenluft, während gleichzeitig die relative Feuchte der Außenluft höher ist als die relative Feuchte der Innenluft.

Luftfeuchte-Tutorial
Feuchtemaße
Die Wetterdateiformate, die WUFI lesen kann, benutzen die relative Feuchte als Maß für den Feuchtegehalt der Luft. Wenn Sie Wetterdaten aus anderen Quellen benutzen, können Ihnen aber auch andere Feuchtemaße begegnen. Im Folgenden werden verschiedene gängige Feuchtemaße vorgestellt. Über die bloßen Definitionen hinaus werden auch die jeweiligen Eigenschaften dieser Feuchtemaße erläutert. Die Kenntnis dieser Details ist nicht notwendig, um eine hygrothermische Simulation durchzuführen, sie ist aber hilfreich zum Verständnis feuchtetechnischer Vorgänge.
Die meisten der folgenden Feuchtemaße hängen nicht nur von der Menge der in der Luft enthaltenen Feuchtigkeit ab, sondern auch von der Temperatur und/oder dem Druck der Luft. Sie ändern sich also nicht nur, wenn Wassermoleküle der Luft hinzugefügt oder aus der Luft entfernt werden, sondern auch wenn sich die Temperatur oder der Druck ändern. Dies ist keine Unzulänglichkeit dieser Feuchtemaße, es ist vielmehr zweckmäßig für die Beschreibung der jeweiligen Eigenschaften feuchter Luft. Sie sollten sich dieser Eigenschaften der verschiedenen Feuchtemaße aber bewusst sein, um Fehlinterpretationen zu vermeiden.
Insbesondere hängt die Wahl eines geeigneten Feuchtemaßes davon ab, ob ausschließlich eine quantitative Aussage über die vorhandene Feuchtemenge beabsichtigt ist, oder auch eine Aussage über eine der Auswirkungen des Feuchtegehalts.
In hygrothermischen Gebäudesimulationen ist der Druck in der Regel der Atmosphärendruck, dessen Schwankungen üblichweise nur vernachlässigbare Auswirkungen auf das Simulationsergebnis haben. Die Druckabhängigkeit kann aber beispielsweise in Druckluftsystemen wichtig sein.
• Wasserdampfpartialdruck
Der Wasserdampfpartialdruck, kurz Wasserdampfdruck oder Dampfdruck, ist der Druck, den der in der Luft enthaltene Wasserdampf zum Gesamtdruck der Luft beiträgt (Daltonsches Gesetz).
Trockene Luft und Wasserdampf können in guter Näherung als ideale Gase behandelt werden, die sich auch in der Mischung "feuchte Luft" gegenseitig nicht beeinflussen. Daher gilt insbesondere für den im betrachteten Luftpaket enthaltenen Wasserdampf das ideale Gasgesetz
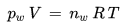
pw [Pa] : Wasserdampfpartialdruck im Luftpaket
V [m3] : Volumen des Luftpakets
nw [mol] : Molzahl der Wasserdampfmoleküle im Luftpaket
R [J/(mol K)] : universelle Gaskonstante, 8.314 J/(mol K)
T [K] : absolute Temperatur des Luftpakets
Auflösen der Gleichung nach dem Partialdruck pw liefert
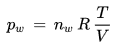
Bei festgehaltenem Verhältnis T/V von Volumen V und Temperatur T eines gegebenen Luftpakets nimmt der Wasserdampfdruck pw also zu, wenn Wassermoleküle der Luft hinzugefügt werden, weil unter diesen Bedingungen der Druck eines Gases proportional zur Anzahl seiner Moleküle ist (Avogadros Gesetz). Der Wasserdampfdruck ist unter diesen Bedingungen ein direktes Maß für die Anzahl der im Luftpaket enthaltenen Wassermoleküle.
Der Wasserdampfdruck kann sich im Allgemeinen aber auch ändern, ohne dass Wassermoleküle hinzugefügt oder entfernt werden. Der Wasserdampfdruck in einem gegebenen Luftpaket nimmt beispielsweise proportional zur Temperatur T zu, wenn T bei festgehaltenem Volumen V und festgehaltener Molekülzahl nw erhöht wird (Gesetz von Amontons, die Moleküle bewegen sich schneller), er nimmt proportional zu 1/V zu, wenn das Volumen V bei festgehaltener Temperatur T und festgehaltener Molekülzahl nw komprimiert wird (Gesetz von Boyle-Mariotte, aufgrund ihrer höheren Dichte treffen die Moleküle häufiger auf die Behälterwand). Der letztere Fall tritt beispielsweise in Luftkompressoren auf: Wenn die Luft so stark komprimiert wird, dass der erhöhte Dampfdruck des enthaltenen Wasserdampfs den Sättigungsdampfdruck bei der aktuellen Temperatur übersteigt, fällt Kondensat aus. Wenn zwei oder alle drei Variablen auf der rechten Seite variieren, beschreibt das ideale Gasgesetz die zugehörige Variation des Wasserdampfdrucks.
In hygrothermischen Simulationen sind üblicherweise weder T noch V festgehalten. Die Temperatur stellt sich nach Maßgabe der Randbedingungen und der hygrothermischen Prozesse ein. Das Volumen eines gegebenen Luftpakets kann sich frei zusammenziehen oder ausdehnen, wenn Temperatur oder Gesamtdruck sich ändern.
Für die aus trockener Luft und Wasserdampf bestehende Mischung "feuchte Luft" gilt ebenfalls das ideale Gasgesetz
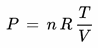
P [Pa] : Gesamtdruck des Luftpakets
(= Summe aus den Partialdrücken ptr der trockenen Luft und pw des enthaltenen Wasserdampfs)
n [mol] : Gesamtmolzahl im Luftpaket
(= Summe aus den Molzahlen ntr der trockenen Luft und nw des enthaltenen Wasserdampfs)
Division des idealen Gasgesetzes für den Wasserdampf durch das ideale Gasgesetz für die feuchte Luft liefert den folgenden Zusammenhang zwischen dem Wasserdampfpartialdruck pw und dem Gesamtdruck P:
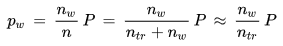
Der Partialdruck des Wasserdampfs ergibt sich also, indem der Gesamtdruck P des Gemisches mit dem Stoffmengenanteil nw/n des Wasserdampfs multipliziert wird. Dies ist das Daltonsche Gesetz.
Die im letzten Schritt vorgenommene Näherung ist in normaler atmosphärischer Luft gerechtfertigt, da in ihr die Molzahl nw des Wasserdampfs gering ist im Vergleich zur Molzahl ntr der trockenen Luft (in gesättigter Luft bei 20 °C kommt ein Wassermolekül auf 43 Luftmoleküle). In diesem Fall ist - bei festgehaltener Molzahl ntr der trockenen Luft und festgehaltenem Gesamtdruck P - der Partialdruck ein direktes Maß für die im Luftpaket enthaltene Molzahl der Wasserdampfmoleküle.
Wie die Formel zeigt, kann sich der Zahlenwert des Partialdrucks auch bei konstanter Anzahl von Wassermolekülen ändern, wenn sich der Gesamtdruck ändert. Er bleibt bei meteorologisch oder technisch vorgegebenem Gesamtdruck jedoch unbeeinflusst von eventuellen Änderungen der Temperatur oder des Volumens des betrachteten Luftpakets.
Die meteorologisch bedingten Änderungen des Gesamtdrucks gehen nur langsam vor sich, ihr Einfluss wird in vielen Messreihen vernachlässigbar sein, muss aber beim Vergleich von Feuchtemessungen verschiedener Zeitperioden oder Standorte unter Umständen berücksichtigt werden.
Der Wasserdampfpartialdruck kann den Sättigungsdampfdruck psat nicht übersteigen, sofern sich Oberflächen in der Nähe befinden, auf denen Feuchte kondensieren kann. Solche Oberflächen sind praktisch immer vorhanden, denn es kann sich beispielsweise um Wandoberflächen handeln (Tauwasserausfall), aber auch um schwebende Staubteilchen, die als Kondensationskerne dienen (Nebelbildung).
Der Sättigungsdampfdruck ist stark temperaturabhängig. Bei 0 °C beträgt er beispielsweise 611 Pa, bei 20 °C beträgt er 2339 Pa. Eine Formel zur Berechnung des Sättigungsdampfdrucks wird weiter unten angegeben.
Anmerkung: Die eben beschriebene Obergrenze für den Feuchtegehalt wird oft so ausgedrückt, dass die Luft bei gegebener Temperatur nur eine bestimmte maximale Feuchtemenge aufnehmen könne. Diese Ausdrucksweise ist irreführend, da sie nahelegt, die Maximalmenge sei durch die Eigenschaften der Luft bestimmt - so als ob die Luft ein Schwamm sei, der die Feuchtigkeit aufsaugt und bei einer bestimmten Menge seine Aufnahmekapazität erschöpft hat. Dies trifft nicht zu - wie oben erwähnt wechselwirken Luft und Wasserdampf so gut wie gar nicht. Der maximal mögliche Wasserdampf-Partialdruck ist beispielsweise in einer reinen Edelgasatmosphäre oder sogar im Vakuum derselbe wie in Luft. Außerdem zeigt die Erfahrung, dass andere flüchtige Flüssigkeiten (etwa Benzin oder Alkohol) auch in "feuchtegesättigte Luft" hinein verdunsten können, so dass offenbar die Vorstellung einer erschöpften Aufnahmekapazität nicht richtig sein kann.
Der maximal mögliche Partialdruck wird vielmehr durch die Eigenschaften des Wasserdampfs selbst bestimmt, nämlich die beim Sättigungs-Partialdruck beginnende Kondensationsfähigkeit. Kurzzeitige Übersättigung kann oft vorkommen, der Partialdruck reduziert sich dann aber infolge Kondensation schnell wieder auf den Sättigungswert (ein Beispiel folgt im nächsten Abschnitt). In besonders reiner Luft ohne nahe Kondensationsflächen (z.B. in der Atmosphäre in großer Höhe) kann der Sättigungsdampfdruck längere Zeit um das Zwei- bis Dreifache überschritten werden.
Fazit: Dampfdruckunterschiede sind die treibenden Kräfte für die Dampfdiffusion, sie bestimmen also die Dampfdiffusion innerhalb des Bauteils und über die Bauteilgrenzen. Die Dampfmenge in der Luft ist durch den Sättigungsdampfdruck beschränkt. Vergleich des aktuellen Dampfdrucks mit dem der aktuellen Temperatur entsprechenden Sättigungsdampfdruck erlaubt die Möglichkeit (und gegebenenfalls die Rate) von Kondensation zu bestimmen.
• Relative Feuchte
Die relative Feuchte ist definiert als das Verhältnis des aktuellen Wasserdampfpartialdruckes in der Luft zu dem der aktuellen Lufttemperatur entsprechenden Sättigungsdampfdruck. Sie wird als Prozentsatz (z.B. 78 %) oder Verhältniszahl (z.B. 0.78) ausgedrückt.
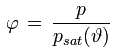
φ [%] oder [-] : relative Feuchte
p [Pa] : Wasserdampfpartialdruck
psat(ϑ) [Pa] : Wasserdampfsättigungsdruck bei der Temperatur ϑ
Die Abhängigkeit der relativen Feuchte von der Anzahl der in der Luft vorhandenen Wassermoleküle unter gegebenen Bedingungen ist der Definition entsprechend dieselbe wie die Abhängigkeit des Wasserdampfpartialdrucks p unter diesen Bedingungen (siehe z.B. die oben beschriebenen Einflüsse von Temperatur, Volumen oder Gesamtdruck). Zusätzlich liegt jedoch eine starke Temperaturabhängigkeit vor: Wenn die Temperatur zunimmt, nimmt auch der temperaturabhängige Sättigungsdampfdruck psat zu, und auch in Situationen, in denen der Wasserdampfdruck p dabei konstant bleibt, nimmt die relative Feuchte ab.
Wenn die relative Feuchte der Luft 100 % erreicht, ist die Luft mit Feuchtigkeit gesättigt und der Partialdruck ist gleich dem Sättigungsdampfdruck. Weitere Feuchtezufuhr führt zur Kondensation der überschüssigen Feuchte (siehe oben). Beachten Sie, dass eine feuchte Oberfläche unter Umständen auch dann Feuchte in die Außenluft abgeben kann, wenn diese bereits gesättigt ist: Sofern die Temperatur der Oberfläche über der Lufttemperatur liegt, kann sie einen höheren Partialdruck aufweisen, so daß aufgrund des Dampfdruckunterschieds ein von der Oberfläche fort gerichteter Diffusionsstrom einsetzt. Dies führt zur Übersättigung der oberflächennahen Luft und Kondensatausfall in der Luft (z.B. in Form von sichtbaren Dampfschwaden).
Der in den Poren eines porösen hygroskopischen Materials adsorbierte Ausgleichswassergehalt hängt ab vom Verhältnis der Adsorptionsrate (wird bestimmt vom Wasserdampfpartialdruck p in der Porenluft) zur Verdunstungsrate (wird im Wesentlichen bestimmt durch den Sättigungsdampfdruck psat über den adsorbierten Wasseroberflächen). Er hängt daher von der relativen Feuchte φ der Porenluft und damit letztlich von der relativen Feuchte der Umgebungsluft ab, der das Material ausgesetzt ist (statt beispielsweise der absoluten Feuchte der Umgebungsluft). Die Feuchtespeicherfunktion beschreibt den Ausgleichswassergehalt daher als Funktion der relativen Feuchte.
Die meisten Instrumente zur Messung des Feuchtegehalts der Luft benutzen feuchtegehaltsabhängige Eigenschaften geeigneter Materialien (z.B. Längenänderungen von Fasern, Änderungen der elektrischen Eigenschaften von Polymeren, usw). Da der Feuchtegehalt dieser Materialien von der relativen Feuchte der Umgebungsluft bestimmt wird, ist das von diesen Instrumenten gemessene Feuchtemaß die relative Feuchte der Luft.
Der in der Definition der relativen Feuchte verwendete Sättigungsdampfdruck psat setzt chemisch reines Wasser und eine flache Wasseroberfläche voraus. Wenn sich gelöste Stoffe (z.B. Salze) im Wasser befinden, oder wenn die Oberfläche konkav gekrümmt ist (z.B. in kleinen Poren), ist der tatsächliche Sättigungsdampfdruck verringert und Sättigungsgleichgewicht tritt schon bei weniger als 100 % relativer Feuchte auf (denn auch unter diesen Umständen wird definitionsgemäß der Sättigungsdampfdruck über reinem Wasser und einer ebenen Wasseroberfläche als Referenz verwendet).
So beträgt beispielsweise der Gleichgewichtsdampfdruck über einer gesättigten Kochsalzlösung bei 20 °C nicht 2339 Pa (wie über reinem Wasser), sondern wegen der geringeren Konzentration der Wassermoleküle in der Lösung nur 1765 Pa, so dass sich in der Luft über der Salzlösung eine relative Feuchte von 1765 Pa / 2339 Pa = 75.4 % einstellt. Eine gesättigte Kochsalzlösung kann daher zur Einstellung und Konstanthaltung dieser relativen Feuchte benutzt werden, was beispielsweise die gezielte Konditionierung einer Materialprobe zur Bestimmung der Feuchtespeicherfunktion bei dieser Feuchte ermöglicht.
Liegt flüssiges Wasser im Porenraum eines porösen Materials vor, dann sind die Wasseroberflächen in den Poren aufgrund der Kapillarkräfte konkav gekrümmte "Menisken". Wegen der stärkeren Bindung der Wassermoleküle in den gekrümmten Wasseroberflächen ist der Gleichgewichtsdampfdruck gegenüber dem Gleichgewichtsdampfdruck über einer ebenen Wasseroberfläche vermindert.
Die relative Feuchte der Porenluft, die im hygrischen Gleichgewicht mit den gekrümmten Menisken der Wasseroberflächen steht, beträgt also weniger als 100 %, wobei der genaue Zahlenwert von der Krümmung der Menisken abhängt.
Andererseits übt ein Meniskus Zugkräfte auf das Porenwasser aus und erzeugt so einen (negativen) Kapillardruck im Wasser, wobei der genaue Zahlenwert ebenfalls von der Krümmung der Menisken abhängt.
Mit anderen Worten: Im hygrischen Gleichgewicht existiert ein mathematischer Zusammenhang zwischen der relativen Feuchte der Porenluft und dem Kapillardruck im Wasser. Da Kapillardruckunterschiede den kapillaren Flüssigtransport antreiben, lässt sich mit gleichem Recht auch sagen, dass Unterschiede in relativer Feuchte den kapillaren Flüssigtransport antreiben. In der Tat benutzen WUFIs Transportgleichungen die relative Feuchte als treibendes Potential, weil sie gegenüber dem Wassergehalt als treibendem Potential Vorteile hat.
Die Kelvin-Gleichung beschreibt den funktionellen Zusammenhang zwischen der relativen Feuchte der Porenluft und dem Kapillardruck im Porenwasser:
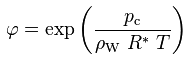
φ [-] : relative Feuchte der Porenluft
pc [Pa] : Kapillardruck im Porenwasser, bezogen auf den Umgebungsdruck
ρW [kg/m3] : Dichte des Wassers, 1000 kg m-3
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
T [K] : absolute Temperatur
Die folgende Tabelle zeigt einige Beispiele für den Zusammenhang zwischen dem Krümmungsradius der Menisken, dem durch die Meniskenkrümmung erzeugten Kapillardruck im Porenwasser und der relativen Feuchte der Porenluft, die sich im Gleichgewicht über den gekrümmten Menisken einstellt:

Der Zusammenhang zwischen der Meniskenkrümmung (Krümmungsradius r) und dem Kapillardruck pc ist gegeben durch pc = 2 σ / r mit der Oberflächenspannung σ (0.072 N/m bei 25°C). Der Zusammenhang zwischen dem Kapillardruck und der relativen Feuchte ist gegeben durch die Kelvin-Gleichung.
In einer Kapillare mit dem Radius rc nimmt ein Meniskus den Krümmungsradius r = rc / cos(γ) an. γ ist der von der Benetzbarkeit des Porenmaterials abhängige Kontaktwinkel zwischen dem Meniskusrand und der Porenwand. Für gut benetzbare Materialien ist cos(γ) ≈ 1 und der in der Tabelle aufgeführte Meniskenradius kann näherungsweise gleich dem Radius der größten gefüllten Poren gesetzt werden.
Wie der Tabelle zu entnehmen ist, beträgt beispielsweise die Gleichgewichtsfeuchte über teilweise gefüllten Poren mit dem Radius 0.005 µm etwa 80 %. Bei einer relativen Porenluftfeuchte von 80 % füllen sich daher die Poren mit Radien unter 0.005 µm infolge "Kapillarkondensation", weil in ihnen bereits bei 80 % relativer Feuchte Übersättigung vorliegt. In den kleinen Poren kann daher bereits bei relativen Feuchten von 80..90 % (je nach Porenradienverteilung des betrachteten Materials) flüssiges Wasser kondensieren, was zu einem starken Anstieg der Ausgleichswassergehalte bei diesen Luftfeuchteniveaus führt, einem typischen Charakteristikum der Feuchtespeicherfunktionen gängiger Materialien.
• Wasserdampfkonzentration, absolute Feuchte
Die Wasserdampfkonzentration (auch: absolute Feuchte) ist das Verhältnis der Masse des in einem Paket feuchter Luft enthaltenen Wasserdampfes zum Volumen des Pakets:
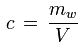
c [g/m3] : Wasserdampfkonzentration, absolute Feuchte
mw [kg] : Masse des im Luftpaket enthaltenen Wasserdampfs
V [m3] : Volumen des Luftpakets
Der Zusammenhang zwischen der Wasserdampfkonzentration und dem Wasserdampfpartialdruck ist durch das ideale Gasgesetz gegeben:
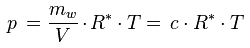
p [Pa] : Wasserdampfpartialdruck
c [kg/m3] : Wasserdampfkonzentration
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
T [K] : absolute Temperatur
nach c aufgelöst also:
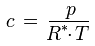
Die Abhängigkeit der Wasserdampfkonzentration von der Anzahl der in der Luft vorhandenen Wassermoleküle unter gegebenen Bedingungen ist demnach dieselbe wie die Abhängigkeit des Wasserdampfpartialdrucks p unter diesen Bedingungen (siehe z.B. die oben beschriebenen Einflüsse von Temperatur, Volumen oder Gesamtdruck). Es liegt jedoch eine zusätzliche Temperaturabhängigkeit vor: Wenn die Temperatur zunimmt (bei festgehaltenem Gesamtdruck, wie es in hygrothermischen Simulationen üblicherweise der Fall ist), nimmt die Wasserdampfkonzentration in einem gegebenen Luftpaket ab, weil sich dann das Volumen des Pakets ausdehnt und die Masse des in der Luft enthaltenen Wassers sich auf ein größeres Volumen V verteilt.
Die Wasserdampfkonzentration kann gemessen werden, indem man mit einem starken Absorber alles Wasser in einem bekannten Luftvolumen absorbiert und durch Wägung die absorbierte Wassermenge bestimmt.
Typische Werte sind 4.8 g/m3 bei 0 °C und Sättigung, und 17.3 g/m3 bei 20 °C und Sättigung.
• Mischungsverhältnis, Wassergehalt, Feuchtegrad
Das Mischungsverhältnis (auch: Wassergehalt, Feuchtegrad) eines gegebenen Pakets feuchter Luft ist das Verhältnis der in diesem Paket enthaltenen Masse des Wasserdampfes zur Masse der trockenen Luft:
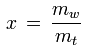
x [kg/kg] : Mischungsverhältnis
mw [kg] : Masse des im Paket enthaltenen Wasserdampfs
mt [kg] : Masse der im Paket enthaltenen trockenen Luft
Das Mischungsverhältnis ändert sich nur dann, wenn Wassermoleküle der Luft hinzugefügt oder entnommen werden. Wenn die Temperatur des Luftpakets zunimmt, vergrößert sich dessen Volumen, aber das Verhältnis zwischen der Anzahl der Wassermoleküle und der Anzahl der Luftmoleküle im Paket bleibt unverändert, also bleibt auch das Verhältnis ihrer Massen unverändert. Dasselbe gilt für Volumenänderungen, die durch Druckänderungen verursacht werden.
Wird beispielsweise feuchte Luft durch ein Rohrsystem mit abschnittsweise unterschiedlichen Temperaturen und Drücken gepumpt, bleibt das Mischungsverhältnis auf dem ganzen Weg dasselbe, solange keine Kondensation oder Verdunstung auftritt.
Der Zusammenhang zwischen dem Mischungsverhältnis und dem Wasserdampfpartialdruck ist gegeben durch die Formel
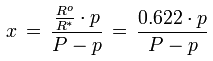
x [kg/kg] : Mischungsverhältnis
Ro [J/(kg K)] : Gaskonstante für trockene Luft, 287.1 J/(kg K)
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
p [Pa] : Wasserdampfpartialdruck
P [Pa] : Luftdruck
• Spezifische Feuchte
Die spezifische Feuchte eines gegebenen Pakets feuchter Luft ist das Verhältnis der in diesem Paket enthaltenen Masse des Wasserdampfes zur Masse der feuchten Luft (d.h. zur Summe der Massen von Wasserdampf und trockener Luft):
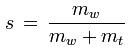
s [kg/kg] : spezifische Feuchte
mw [kg] : Masse des im Paket enthaltenen Wasserdampfs
mt [kg] : Masse der im Paket enthaltenen trockenen Luft
Ebenso wie beim Mischungsverhältnis ändert sich die spezifische Feuchte nur dann, wenn Wassermoleküle der Luft hinzugefügt oder entnommen werden. Besteht die feuchte Luft fast nur aus Wasserdampf und wenig Luft, nimmt die spezifische Feuchte Werte nahe 1 an, während das Mischungsverhältnis sich dem Wert Unendlich nähert.
Der Zusammenhang zwischen der spezifischen Feuchte und dem Wasserdampfpartialdruck ist durch die folgende Formel gegeben:
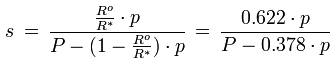
s [kg/kg] : spezifische Feuchte
Ro [J/(kg K)] : Gaskonstante für trockene Luft, 287.1 J/(kg K)
R* [J/(kg K)] : Gaskonstante für Wasserdampf, 461.5 J/(kg K)
p [Pa] : Wasserdampfpartialdruck
P [Pa] : Luftdruck
• Taupunkttemperatur
Die Taupunkttemperatur feuchter Luft ist jene Temperatur, auf welche ein Paket feuchter Luft bei konstantem Gesamtdruck und konstanter Anzahl enthaltener Wassermoleküle gekühlt werden müsste, damit der enthaltene Wasserdampf Sättigung erreicht und zu kondensieren beginnt.
Der größte bei einer gegebenen Temperatur ϑ auftretende Wasserdampfdruck ist, wie oben erwähnt, der Sättigungsdampfdruck psat(ϑ).
Die Taupunkttemperatur ϑTau von Luft, die Wasserdampf mit dem Dampfdruck p enthält, ist die fiktive Temperatur, für die gilt
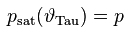
psat [Pa] : Sättigungsdampfdruck
ϑTau [°C] : Taupunkttemperatur
p [Pa] : aktueller Wasserdampfpartialdruck
Die Taupunkttemperatur ist also ein Maß für den Wasserdampfpartialdruck. Sie drückt den Wasserdampfpartialdruck lediglich durch jene Temperatur aus, die man in einer Sättigungsdampfdruckformel einsetzen muss, damit die Formel den betreffenden Wasserdampfpartialdruck liefert. Die obigen Bemerkungen zur Temperatur- und Druckabhängigkeit des Wasserdampfpartialdrucks treffen daher auch auf die Taupunkttemperatur zu.
Bei einem Wasserdampfpartialdruck von 611 Pa beträgt die Taupunkttemperatur 0 °C, bei 2339 Pa beträgt sie 20 °C .
Die Taupunkttemperatur ist ein geeignetes Feuchtemaß zur Beurteilung, wann Kondensation auftreten kann.
Die Taupunkttemperatur der Luft kann direkt mit einem gekühlten Taupunktspiegel gemessen werden.
• Feuchtkugeltemperatur
Die Feuchtkugeltemperatur ist die Temperatur, die ein mit einem befeuchteten Stoffüberzug versehenes Thermometer anzeigt. Sie liegt aufgrund der Verdunstungskühlung unter der von einem trockenen Thermometer angezeigten Lufttemperatur. Das Ausmaß der Kühlung ist abhängig von der Verdunstungsrate, welche in feuchter Luft kleiner ist als in trockener Luft. Die Umrechnung in andere Feuchtemaße geschieht mittels Psychrometertabellen oder empirischer Psychrometerformeln.
Die Feuchtkugeltemperatur der Luft kann direkt mit einem entsprechend ausgestatteten Thermometer gemessen werden.
Zusammenfassung
Die einzigen geläufigen Feuchtemaße, die sich nur dann ändern, wenn dem betrachteten Luftpaket Wassermoleküle hinzugefügt oder entzogen werden, sind das Mischungsverhältnis x und die spezifische Feuchte s. Diese Feuchtemaße beschreiben also den Feuchtegehalt im engeren Sinn.
Die anderen Feuchtemaße ändern sich zusätzlich bei Änderungen von Druck, Volumen oder Temperatur. Dies kann für den beabsichtigten Zweck erwünscht oder unerwünscht sein. Die folgende Tabelle gibt einen Überblick darüber, von welchen zusätzlichen Variablen die einzelnen Feuchtemaße beeinflusst werden (konstante Anzahl von Molekülen trockener Luft im Luftpaket stets vorausgesetzt).
Dabei wird der in der Hygrothermik häufig vorkommende Fall vorausgesetzt, dass der Gesamtdruck P vorgegeben ist, so dass die Formeln soweit möglich unter Verwendung von P formuliert sind. Falls stattdessen Temperatur und Volumen vorgegeben sind, bietet es sich an, die Formeln unter Verwendung des idealen Gasgesetzes für den Gesamtdruck entsprechend umzuformulieren.
- Das Mischungsverhältnis x
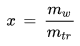
ändert sich bei
• Hinzufügen oder Entfernen von Wassermolekülen
. - Die spezifische Feuchte s
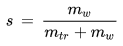
ändert sich bei
• Hinzufügen oder Entfernen von Wassermolekülen
. - Der Wasserdampf-Partialdruck p
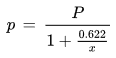
ändert sich bei
• Hinzufügen oder Entfernen von Wassermolekülen
• Änderung des Gesamtdrucks P
. - Die Taupunkttemperatur ϑTau
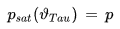
ändert sich
• wie der Partialdruck p
. - Die Wasserdampfkonzentration c
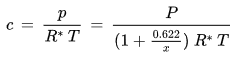
ändert sich bei
• Hinzufügen oder Entfernen von Wassermolekülen
• Änderung des Gesamtdrucks P
• Änderung der Temperatur T
. - Die relative Feuchte φ
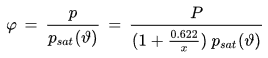
ändert sich bei
• Hinzufügen oder Entfernen von Wassermolekülen
• Änderung des Gesamtdrucks P
• Änderung der Temperatur ϑ
- bleibt das Mischungsverhältnis x unverändert, da keine Verdunstung oder Kondensation stattfindet
- bleibt der Wasserdampf-Partialdruck p unverändert, weil das Mischungsverhältnis x und der Gesamtdruck P unverändert bleiben
- nimmt die Wasserdampfkonzentration c ab, weil zwar der Wasserdampf-Partialdruck p unverändert bleibt, aber die Temperatur T zunimmt
- nimmt die relative Feuchte φ ab, weil zwar der Wasserdampf-Partialdruck p unverändert bleibt, aber die Temperatur ϑ und damit der Sättigungsdampfdruck psat(ϑ) zunimmt.
- bleibt das Mischungsverhältnis x unverändert, da keine Verdunstung oder Kondensation stattfindet
- verringert sich der Wasserdampf-Partialdruck p proportional zum Gesamtdruck P
- nimmt die Wasserdampfkonzentration c proportional zum Gesamtdruck P (oder zum Wasserdampf-Partialdruck p) ab. Falls sich auch die Temperatur ändert, besteht eine zusätzliche Temperaturabhängigkeit.
- nimmt die relative Feuchte φ proportional zum Gesamtdruck P (oder zum Wasserdampf-Partialdruck p) ab. Falls sich auch die Temperatur ändert, besteht eine zusätzliche Temperaturabhängigkeit.
Der Sättigungsdampfdruck ist der Wasserdampfpartialdruck, der sich bei einer gegebenen Temperatur im Gleichgewicht über einer flachen Wasseroberfläche einstellt. Es existiert eine Vielzahl verschieden aufwändiger und verschieden genauer empirischer Formeln zur Berechnung des Sättigungsdampfdrucks. Einen günstigen Kompromiss zwischen Aufwand und Genauigkeit bieten Formeln vom Magnus-Typ. Sie können außerdem explizit nach der Taupunkttemperatur aufgelöst werden, die einem gegebenen Wasserdampfpartialdruck entspricht. Ein Beispiel für eine Magnus-Formel und ihre Inverse ist
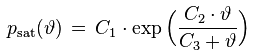
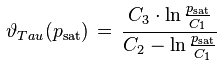
psat [Pa] : Sättigungsdampfdruck
ϑ [°C] : Temperatur
ϑTau [°C] : Taupunkttemperatur
mit dem folgenden Koeffizientensatz [1]:

Über einer konkav gekrümmten Wasseroberfläche (z.B. dem Meniskus in einer teilweise gefüllten Materialpore) ist der Sättigungsdampfdruck kleiner als über einer flachen Oberfläche, siehe Kelvin-Gleichung. Die sehr geringe Abhängigkeit des Sättigungsdampfdrucks vom Luftdruck wird üblicherweise vernachlässigt.
Literatur:
[1] Deutscher Wetterdienst: Aspirations-Psychrometer-Tafeln.
5. Auflage, Vieweg
Update: 2019-05-02, TS
Update: 2020-09-02, TS