Grundlagen: Feuchtetransport in Bauteilen - Rechnerische Simulation mit Hilfe des Modells WUFI (Deutsch)
Posted: Mon Nov 12, 2018 6:02 am -1100
Grundlagen: Feuchtetransport in Bauteilen
Rechnerische Simulation mit Hilfe des Modells WUFI
1. Einleitung
Beim Thema "Feuchtetransport durch Bauteile" denkt der Praktiker in erster Linie an Dampfdiffusion, Taupunkt und das Glaser-Verfahren in der DIN 4108. Wird ein Bauteil "nach Glaser" als unbedenklich eingestuft, so ist in der Regel damit für den Planer alles erledigt.
Erst wenn dennoch unerwartet Feuchteschäden auftreten, oder das geplante Bauteil bei der Normberechnung nach Glaser durchfällt, wird nach alternativen Beurteilungsmöglichkeiten gesucht. Da die winterliche Tauwasserbildung durch Dampfdiffusion (ausschließlich damit befasst sich Glaser) nur eine Feuchtebelastung unter vielen darstellt, kann eine positive Bewertung nach DIN 4108 eine Feuchtesicherheit vortäuschen, die gar nicht vorhanden ist. Probleme mit anderen Feuchteeinwirkungen, wie z.B. durch Raumluftkonvektion, Niederschlag oder aufsteigende Feuchte sind hierbei nicht berücksichtigt. Das gleiche gilt für die Baufeuchte, die beim heutigen Termindruck auf den Baustellen eine zunehmende Brisanz erfährt.
Um auch diese Einflüsse erfassen zu können, muss von dem einfachen stationären Bewertungsverfahren nach Glaser zur realitätsnahen Simulation der Feuchteverhältnisse in Bauteilen übergegangen werden. Zu diesem Zweck sind in den letzten Jahren neue instationäre Rechenverfahren entwickelt und experimentell validiert worden, deren Zuverlässigkeit inzwischen so groß ist, dass sich ihr Einsatz auch in der Praxis immer mehr durchsetzt. Dieser Tatsache wird auch in der Neufassung der DIN 4108 Teil 3 durch entsprechende Hinweise Rechnung getragen.
Im Folgenden werden die Auswirkungen von erhöhter Feuchte und von Feuchtewechselbeanspruchungen in Bauteilen aufgezeigt und die physikalischen Grundlagen des Feuchteverhaltens von Bauteilen beschrieben. Anhand des inzwischen weit verbreiteten instationären Simulationsmodells WUFI werden anschließend die Voraussetzungen in bezug auf die Material- und Klimadaten sowie die Genauigkeit der Berechnungen analysiert.
2. Feuchtewirkungen in Bauteilen
Die Gebrauchstauglichkeit und die Dauerhaftigkeit von Bauteilen und Baustoffen kann durch Feuchteeinwirkungen beeinträchtigt werden, z.B.:
2.1 Feuchtebedingte Wärmeverluste
In der Regel sind die Wärme- und Feuchtetransportprozesse in Gebäuden stark gekoppelt. Dies zeigt sich besonders deutlich beim Feuchteeinfluss auf die Wärmedämmung von Bauteilen. Bild 1 zeigt den Anstieg der Wärmeleitfähigkeit von drei verschiedenen Baustoffen in Abhängigkeit vom Wassergehalt nach [1].
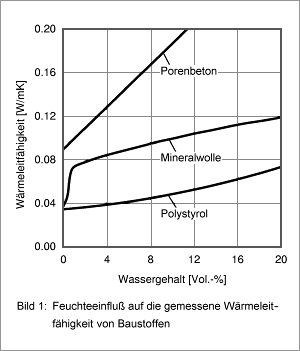
Während die Wärmeleitung mineralischer Wandbildner, wie bei dem hier dargestellten Porenbeton, linear mit dem Wassergehalt ansteigt, ist der Anstieg bei Polystyrol-Hartschaum leicht progressiv.
Überraschend ist der starke Anstieg der Wärmeleitfähigkeit von Mineralwolle schon bei sehr kleinem Wassergehalt. Dies ist auf die starke Feuchteverlagerung durch Dampfdiffusion nach Anlegen eines Temperaturgradienten in der Mineralwolle zurückzuführen. Hier handelt es sich um so genannte instationäre Latentwärmeeffekte, bedingt durch die Phasenwechsel der Materialfeuchte während der Messung im Plattenapparat. Diese Latentwärmeeffekte sind in der Regel kurzfristiger Natur und haben nichts mit der realen Wärmeleitfähigkeit des Dämmstoffes zu tun. Da ihr Einfluss stark von den an die Wärmedämmung angrenzenden Bauteilschichten abhängt, können sie nicht dem Dämmstoff selbst zugeordnet werden [2].
Die Darstellung der Wärmeleitfähigkeit für die Mineralwolle in Bild 1 ist daher als Stoffeigenschaftsfunktion sowohl für instationäre Berechnungen als auch für die Ermittlung des stationären Wärmedurchgangskoeffizienten (U-Wert; früher k-Wert) wenig geeignet. Durch entsprechende Vorkehrungen bei der Messung im Plattenapparat lässt sich jedoch die echte Wärmeleitfähigkeit der Mineralwolle ermitteln. Ergebnisse aus solchen Untersuchungen belegen, dass die Wärmeleitfähigkeit der Mineralwolle ohne Latentwärmeeffekte eine ganz ähnliche Feuchteabhängigkeit zeigt, wie die von Polystyrol-Hartschaum in Bild 1. Ähnliches gilt auch für andere diffusionsoffene Dämmstoffe.
2.2 Mechanische Beanspruchung durch hygrothermische Wechsellast
Ein Beispiel für den stark instationären Charakter der gekoppelten Temperatur- und Feuchtewirkungen sind die mechanischen Belastungen durch thermische und hygrische Verformungen bzw. die daraus resultierenden Eigenspannungen in Außenputzen auf Wärmedämmverbundsystemen. Im Tagesverlauf sind diese Putzoberflächen Temperatur- und Feuchteschwankungen von bis zu 40 K und 80 % r.F. ausgesetzt [3].
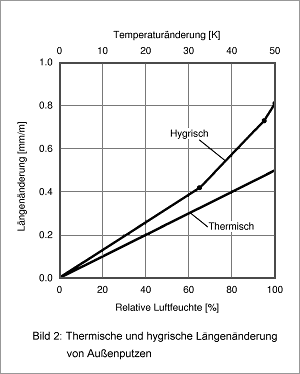
Bild 2 zeigt den Vergleich zwischen thermischer und hygrischer Längenänderung von solchen Außenputzen. Die abgebildeten Werte stellen den Durchschnitt aus Labormessungen an über 20 Proben unterschiedlicher Hersteller dar. Übertragen auf die Verhältnisse am Bau würde dies bei freier Verformbarkeit der Außenputze eine thermisch bedingte Längenänderung von 0,4 mm/m und eine noch größere hygrische Dilatation von 0,7 mm/m bedeuten. Beide Prozesse sind jedoch häufig gegenläufig, da der Putz bei einer Erhöhung der Temperatur austrocknet, was die thermisch bedingte Ausdehnung mit einer gewissen Zeitverzögerung durch hygrisches Schwinden kompensiert. Da die Putzoberflächen jedoch in der Regel nicht frei beweglich sind, kommt es zu Spannungen und bei Überschreiten der Festigkeit zu Rissen oder Ablösungen vom Untergrund.
Weitere Beispiele für Bauschäden aufgrund von hygrothermischen Wechselbeanspruchungen sind Salz- und Frostschäden. Salze kristallisieren unterhalb einer für die Salzart typischen relativen Feuchte aus der Lösung. Wird umgekehrt dieser Kristallisationspunkt wieder überschritten, ziehen sie Wasserdampf aus der Umgebung an und gehen wieder in Lösung. Diese Vorgänge finden auch in den Porenräumen von salzhaltigen Baustoffen statt. Da die Kristallisation dort jedoch durch das enge Porengefüge behindert wird, können erhebliche Kristallisationsdrücke entstehen, die bei einem häufigen Feuchtewechsel zum Zermürben des Materials führen. Je nach Löslichkeit des Salzes spielt sich dieser Prozess an der Oberfläche oder einige Millimeter bis Zentimeter darunter ab und führt entweder zu einem oberflächlichen Absanden der Bausubstanz oder zur Schalenbildung durch Entfestigung der tiefer liegenden Schichten [4]. Frost kann ganz ähnliche Schadensbilder erzeugen, wobei in diesem Fall die Eiskristalle die Rolle der Salzkristalle übernehmen. Ausschlaggebend sind hier die Temperaturwechsel um den Gefrierpunkt und der Wassergehalt in der Frostzone [5].
Die vorangegangenen Beispiele zeigen die Bedeutung von hygrothermischen Wechselbeanspruchungen für die Gebrauchstauglichkeit und die Dauerhaftigkeit von Baustoffen und Bauteilen. Eine genaue Erfassung der wärme- und feuchtetechnischen Prozesse in Baustoffen und Bauteilen ist deshalb nicht nur wünschenswert sondern dringend erforderlich. Beurteilungen mit den bisher eingeführten, ausschließlich auf der Dampfdiffusion basierenden Berechnungsmethoden, wie z.B. dem Glaser-Verfahren, sind hierfür nur in Ausnahmefällen geeignet. Die rechnerische Simulation des instationären Temperatur- und Feuchteverhaltens unter Berücksichtigung aller wesentlichen Transportmechanismen bei natürlichen Klimabedingungen ist inzwischen jedoch so weit entwickelt und auch in der Praxis erprobt, dass ihre konsequente Anwendung in vielen Bereichen des Hochbaus sinnvoll erscheint. Unter diesem Gesichtspunkt sind die folgenden Ausführungen primär zu verstehen.
3. Feuchtespeicher- und Feuchtetransportmechanismen
Für die Anwendung von Simulationsverfahren zur instationären Berechnung des Wärme- und Feuchteverhaltens von Bauteilen sind Grundkenntnisse in bezug auf die Speicher- und Transporteigenschaften von Baustoffen notwendig. Da die Wärmespeicherung und die Wärmeleitung hinlänglich bekannt sind und der Wärmetransport durch Dampfdiffusion mit Phasenwechsel (Latentwärmeeffekt) im Zusammenhang mit dem Feuchtetransport zu sehen ist, wird hier ausschließlich auf die Feuchtephänomene eingegangen. Für die genauere Analyse von Frost-Tau-Prozessen, bei denen die Schmelzwärme und die wärmetechnischen Eigenschaften des Eises eine Rolle spielen, wird auf die Erläuterungen in [2] verwiesen.
3.1 Feuchtespeicherung
Man unterscheidet hygroskopische und nicht hygroskopische Baustoffe. Ist ein Baustoff hygroskopisch, dann nimmt er vom trockenen Zustand aus solange Wasserdampf aus der Luft auf, bis er seine Ausgleichsfeuchte bei den jeweiligen Umgebungsbedingungen erreicht hat. Da die Wasserdampfsorption in erster Linie von der umgebenden relativen Luftfeuchte abhängt, während die Umgebungstemperatur einen demgegenüber geringeren Einfluss hat, wird die hygroskopische Feuchtespeicherung in Form von stoffspezifischen Sorptionskurven dargestellt.
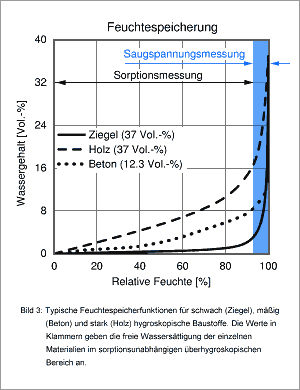
Bild 3 zeigt die Verläufe solcher Sorptionskurven (auch Sorptionsisothermen genannt) für drei in ihrer Hygroskopizität sehr unterschiedliche Baustoffe. Die Sorptionsisothermen werden durch Lagerung der Baustoffproben bei verschiedenen Umgebungsbedingungen im Labor bestimmt. Die obere Grenze des Messbereichs liegt bei etwa 95% r.F., da eine höhere Luftfeuchte wegen der Regelungscharakteristika der meisten Klimakammern zur Betauung der Proben führen würde.
Darüber hinaus bis zur freien Wassersättigung im sog. überhygroskopischen Bereich muss deshalb auf die in [6] beschriebene Saugspannungsmessung zurückgegriffen werden. Bei dieser Messmethode werden Baustoffproben zunächst durch Wasserlagerung frei (d.h. drucklos) gesättigt. Anschließend wird das Wasser in mehreren Druckstufen bis max. 100 bar entfernt, wobei sich bei jeder Druckstufe ein Gleichgewichtswassergehalt einstellt. Die Auswertung dieser Messung ergibt eine überhygroskopische Feuchtespeicherfunktion (dargestellt im blau hinterlegten Bereich in Bild 3), die nahtlos an die klassische Sorptionsisotherme anschließt. Bei grobporigen mineralischen Baustoffen wie z.B. Ziegel ist der überhygroskopische Wassergehaltsbereich größer als der hygroskopische, so dass für genaue Analysen auf Saugspannungsmessungen nicht verzichtet werden kann. Bei feinporigen Materialien wie z.B. Beton ist die Sorptionsfeuchte bei 93% r.F. bereits so hoch, dass der Verlauf im überhygroskopischen Bereich bis zur freien Wassersättigung ohne Genauigkeitsverlust extrapolierbar ist. Holz und Holzwerkstoffe sorbieren ebenfalls schon im hygroskopischen Bereich große Feuchtemengen, so dass auch dort eine Extrapolation bis zur freien Wassersättigung in der Regel ausreicht.
Bei nicht hygroskopischen Baustoffen, wie z.B. Glas, Metall oder einigen Schaumkunststoffen, lagert sich ohne Taupunktsunterschreitung kein Wasser ein. Sie trocknen bei Umgebungsbedingungen unter 100% relativer Feuchte vollständig aus.
3.2 Feuchtetransport
Der Feuchtetransport erfolgt in porösen Baustoffen im Wesentlichen durch Dampfdiffusion, Oberflächendiffusion und Kapillarleitung. In Baustoffen, die kein starres Porengefüge besitzen, wie z.B. Kunststoffe, findet aufgrund der Einlagerung von Wassermolekülen zwischen die polymeren Makromoleküle die so genannte Lösungsdiffusion statt. Bisherige Erfahrungen zeigen, dass diese Art der Diffusion am ehesten durch den Dampfdiffusionsansatz beschreibbar ist, wobei der Diffusionswiderstand im Gegensatz zur normalen Dampfdiffusion von der Umgebungsfeuchte abhängt.
Andere Transportphänomene, wie z.B. Sickerströmung durch Gravitation im nicht wassergesättigten Porenraum oder Wanderung von Wassermolekülen durch elektrische Felder oder osmotische Drücke sind bislang nur unzureichend berechenbar. Da sie nur in Ausnahmefällen eine Rolle spielen, werden sie hier nicht betrachtet. Ebenfalls nicht berücksichtigt werden Konvektionsvorgänge, wie z.B. das Durchströmen von Bauteilen mit feuchter Raumluft aufgrund von Luftdruckunterschieden zwischen innen und außen. Da die Luftdichtheit eine zentrale Anforderung an die Gebäudehülle darstellt, findet die Luftkonvektion in der Praxis ausschließlich unplanmäßig durch Fehlstellen oder ungeeignete Bauteilschichten statt. Sie ist deshalb kaum vorab quantifizierbar und ließe sich auch nur durch dreidimensionale strömungsmechanische Simulationsprogramme in realistischer Weise erfassen. (Das Luftinfiltrationsmodell in WUFI erlaubt eine stark vereinfachte Berücksichtigung von Undichtheiten)
Das Zusammenspiel der oben genannten dominierenden Feuchtetransportphänomene wird in Bild 4 anhand einer Zylinderkapillare in einem Wandausschnitt erläutert. Auf beiden Seiten der betrachteten Kapillare sollen bauübliche Randbedingungen herrschen, d.h. der Dampfdruck sei innen größer als außen und die relative Luftfeuchte sei außen höher als innen. Ist der Baustoff ausreichend trocken oder nicht hygroskopisch, dann diffundiert der Wasserdampf entsprechend dem Dampfdruckgefälle von innen nach außen.
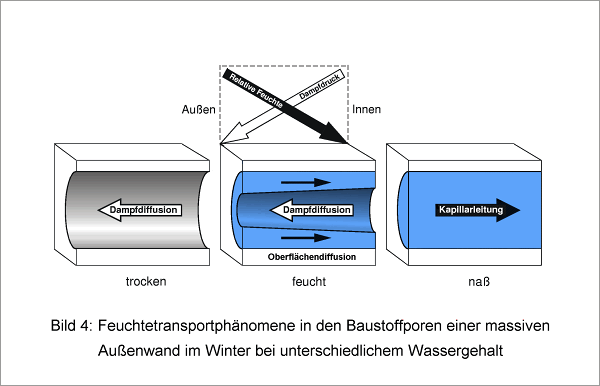
Enthält der Baustoff genügend hygroskopische Feuchte, so dass der Sorbatfilm an den Porenwandungen beweglich wird (dies ist etwa ab 60% r.F. der Fall), dann findet neben der normalen Dampfdiffusion auch die so genannte Oberflächendiffusion durch sorbiertes Wasser an den Porenwandungen statt. Da die Dicke und damit Beweglichkeit der sorbierten Molekülschicht mit der relativen Feuchte zunimmt, erfolgt wie in [6] nachgewiesen ein Feuchtetransport im Sorbatfilm entgegen dem Dampfdruckgefälle von Bereichen höherer Konzentration in Bereiche mit geringerer Konzentration an sorbiertem Wasser. Die treibende Kraft für die Oberflächendiffusion ist daher die relative Feuchte und nicht der Dampfdruck. Unter den hier angenommenen Randbedingungen verlaufen Dampfdiffusion und Oberflächendiffusion in entgegengesetzte Richtungen. Bei der Oberflächendiffusion handelt es sich also um einen Flüssigtransport und nicht um eine Dampfdiffusion in der Gasphase. Dennoch ist es häufig zweckmäßig, die Oberflächendiffusion der Dampfdiffusion zuzuschlagen, z.B. durch Verwendung des im Feuchtbereich (wet-cup) nach DIN 52615 ermittelten µ-Wertes. Dieses Vorgehen führt zu ähnlichen Rechenergebnissen wie die strikte Trennung beider Transportphänomene, wenn in der betrachteten Bauteilschicht keine großen Temperaturgradienten auftreten.
Bei überhygroskopischer Feuchte im Material, beispielsweise infolge von Schlagregen, kommt es bei Füllung der Poren zur so genannten Kapillarleitung, die die effizienteste Form des Feuchtetransports darstellt. Die treibende Kraft ist hier der kapillare Unterdruck, der sich aufgrund der Oberflächenspannung des Wassers im Meniskus an der Grenzfläche zwischen Porenluft und Wasser bildet. Der kapillare Unterdruck steht in einem funktionalen Zusammenhang mit der relativen Feuchte der Porenluft über dem Meniskus, d.h. der treibenden Kraft in der flüssigen Phase kann eine bestimmte relative Luftfeuchte in der Gasphase zugeordnet werden. Alternativ zum kapillaren Unterdruck kann deshalb auch die relative Feuchte als Transportpotential für die Kapillarleitung verwendet werden.
Das Beispiel zeigt deutlich die häufig entgegengesetzten Transportrichtungen von Dampfdiffusion und Flüssigtransport. Die Dampfdiffusion erfolgt meist von warm nach kalt, während der Flüssigtransport weitgehend temperaturunabhängig von feucht nach trocken gerichtet ist. Dieses Phänomen, das jedem Praktiker von der kapillaren Rückleitung (auch kapillare Entspannung genannt) in mineralische Baustoffe bei winterlicher Tauwasserbildung bekannt sein dürfte, muss auch in einem Berechnungsmodell entsprechend der vorangegangenen Analyse korrekt erfasst werden. Das bedeutet, dass für Dampfdiffusion und Flüssigtransport unterschiedliche Triebkräfte angesetzt werden müssen. Besonders vorteilhaft erweist sich in diesem Zusammenhang die Wahl von Temperatur und relativer Feuchte als Transportpotentiale. Der Dampfdruck als treibende Kraft für die Diffusion ist durch beide Größen eindeutig bestimmt. Beide Potentiale sind über den Bauteilquerschnitt stetig, d.h. es treten keine Sprünge an den Materialgrenzen auf, wie das beispielsweise beim Wassergehalt der Fall ist. Auch die im folgenden beschriebenen hygrothermischen Stoffkennwerte und die Randbedingungen lassen sich mit ihrer Hilfe auf einfache Weise definieren.
4. Hygrothermische Stoffkennwerte
Die Ergebnisse einer rechnerischen Simulation sind immer nur so gut wie die zugrunde gelegten Materialparameter. Nachdem der Mangel an zuverlässigen Stoffkennwerten lange Zeit die Akzeptanz moderner Rechenverfahren behindert hat, soll hier gezeigt werden, welche Parameter für die verschiedenen Fragestellungen wirklich notwendig sind. In der Regel sind für die instationäre Berechnung der Temperaturfelder folgende Stoffkennwerte erforderlich:
Falls der Einfluss der Materialfeuchte auf den Wärmedurchgangskoeffizienten (U-Wert) quantifiziert werden soll, muss die Wärmeleitfähigkeit, wie in Bild 1 gezeigt, als Funktion des Wassergehalts eingegeben werden. Angaben dazu finden sich in [1] bzw. in der WUFI-Materialdatenbank. Liegt das Hauptaugenmerk auf dem Feuchteverhalten des Bauteils, dann reicht die Eingabe des Rechenwertes lambda_R, der den praktischen Feuchtegehalt des jeweiligen Baustoffes schon enthält. Das heißt, im Normalfall können alle notwendigen thermischen Stoffkennwerten der DIN 4108-4 oder den entsprechenden Baustoffzulassungen entnommen werden.
Die feuchtetechnischen Kennwerte, die für alle Baustoffe, also auch für nicht hygroskopische Materialien, vorhanden sein müssen, sind:
Die µ-Werte für eine große Anzahl von Baustoffen sind ebenfalls in der DIN 4108-4 enthalten. Die Porosität kann aus Rohdichte und Reindichte oder aus der maximalen Wassersättigung ermittelt werden. Sie spielt allerdings nur dann eine Rolle, wenn der Baustoff Wasser oder Wasserdampf in sein Porengefüge aufnehmen kann. Mit den bisher genannten Materialdaten ist jedoch lediglich eine Art instationäre Glaser-Berechnung möglich, weil noch kein Feuchtespeichervermögen und keine Flüssigtransportvorgänge berücksichtigt sind.
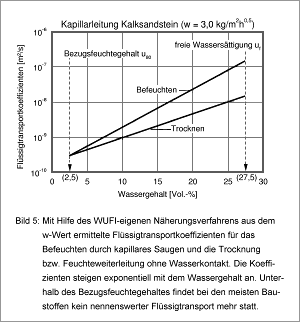
Soll das Verhalten von hygroskopischen, kapillaraktiven Baustoffen korrekt erfasst werden, sind außerdem noch die bereits in Bild 3 gezeigte Feuchtespeicherfunktion und die in Bild 5 dargestellten feuchteabhängigen Flüssigtransportkoeffizienten erforderlich. Bei diesen Koeffizienten hat sich die im Bild gezeigte prozessabhängige Differenzierung als vorteilhaft erwiesen. Das hängt damit zusammen, dass der Befeuchtungsvorgang von mineralischen Baustoffen in Kontakt mit Wasser deutlich schneller abläuft als die kapillare Weiterverteilung bzw. Trocknung nach Unterbrechung der Wasserzufuhr.
Diese zusätzlichen Parameter zur Beschreibung der hygroskopischen und kapillaren Eigenschaften sind inzwischen für zahlreiche Baustoffe in einschlägigen Datenbanken (z.B. WUFI-Datenbank) vorhanden. Die messtechnische Bestimmung von Feuchtespeicherfunktion und Flüssigtransportkoeffizienten ist etwas aufwändig [6], so dass sie für den Praktiker im Normalfall nicht in Frage kommt.
In vielen Fällen können jedoch Näherungsverfahren eingesetzt werden, um diese Kenndaten aus anderen, bekannten Kenndaten abzuleiten. Sind z.B. die kapillaraktiven Materialschichten in einem Bauteil nicht in direktem Kontakt, oder wird diese Kontaktschicht nicht langfristig nass (d.h. findet kein merklicher kapillarer Feuchteaustausch über die Kontaktschicht statt), dann werden mit Hilfe der in WUFI [2] implementierten Approximationsmöglichkeit für die Feuchtespeicherfunktion aus dem Bezugsfeuchtegehalt u80 (Gleichgewichtsfeuchte bei 80% r.F.) gemäß DIN 52620 und der freien Wassersättigung uf ausreichend genaue Rechenergebnisse erzielt.
Ähnliches gilt für die ebenfalls in WUFI integrierte Approximation der Flüssigtransportkoeffizienten (Bild 5) aus dem Wasseraufnahmekoeffizienten (w-Wert) nach DIN 52617.
Für die meisten praktischen Anwendungen können also hygroskopische und kapillaraktive Baustoffe durch folgende - über die Standardstoffkennwerte in DIN 4108-4 hinausgehende - Materialparameter ausreichend genau spezifiziert werden:
Die freie Wassersättigung ist der Wassergehalt, der bei der w-Wert-Messung im Zustand der Durchfeuchtung bestimmt wird.
Da alle Materialeigenschaften von Baustoffen herstellungs- oder verarbeitungsbedingten Schwankungen unterworfen sind, ist es zweckmäßig, die Stoffkennwerte bei der Berechnung analog zu den Vorgaben in der DIN 4108-4 in bestimmten Grenzen zu variieren und den Einfluss dieser Variation auf die Rechenergebnisse zu dokumentieren. Stellt sich der Einfluss eines Materialparameters im betrachteten Anwendungsfall als gering heraus, dann erübrigt sich eine exakte Bestimmung von selbst. Hat der Einfluss des jeweiligen Kennwertes jedoch eine entscheidende Bedeutung für die Interpretation der Ergebnisse, sind Norm- oder Literaturdaten weniger geeignet. Hier sind genaue Messungen der entsprechenden Stoffeigenschaften vorzuziehen.
5. Klima- und Übergangsbedingungen
Jedes Bauteil steht über seine Oberflächen in hygrothermischer Wechselwirkung mit der Umgebung. Das heißt, dass nicht nur die Umgebung auf das Bauteil einwirkt, sondern umgekehrt auch das Bauteil auf die Umgebung, wie z.B. durch Abgabe von gespeicherter Wärme oder durch sorptive Pufferung von Raumluftfeuchte. Diese Tatsache ist bei der Formulierung der Randbedingungen zu beachten.
Grundsätzlich sind drei Bereiche zu unterscheiden: die äußeren Umgebungsbedingungen über sowie unter der Geländeoberkante und die Innenraumverhältnisse. In allen drei Fällen sind, bedingt durch die jeweiligen Austauschprozesse mittels Konvektion und Strahlung bzw. Leitung und Diffusion, unterschiedliche Oberflächenübergangsbedingungen anzusetzen.
5.1 Außenklima
Die auf ein Bauteil einwirkenden Außenklimabedingungen sind die Lufttemperatur, die Luftfeuchte, sowie die Sonnenstrahlung und der Niederschlag. Die Strahlungs- und Niederschlagsbelastung ist abhängig von der Neigung und Orientierung des Bauteils und muss auf die vorliegenden Verhältnisse umgerechnet werden. Zur Ermittlung des Schlagregens sind zusätzlich Windgeschwindigkeit und Windrichtung sowie Kenntnisse der Gebäudeumströmungsverhältnisse erforderlich. Soll die langwellige Abstrahlung berücksichtigt werden, müssen auch Daten zur terrestrischen und atmosphärischen Gegenstrahlung vorliegen.
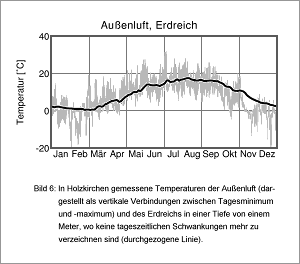
Die täglichen Schwankungen der Witterungsverhältnisse, dargestellt am Beispiel der Lufttemperatur in Bild 6, erfordern in der Regel kurzfristige Betrachtungsintervalle. Für hygrothermische Simulationsrechnungen hat sich der Einsatz von Stundenmittelwerten als günstig erwiesen [7]. Dafür stehen beispielsweise Test-Referenzjahre TRY des Deutschen Wetterdienstes (ohne Regen) oder Hygrothermische Referenzjahre HRY des IBP (mit Regen) zur Verfügung, die jeweils typische Klimabedingungen für entsprechend eingeteilte Klimaregionen der Bundesrepublik beinhalten. Feuchteprobleme treten jedoch in der Regel nicht bei durchschnittlicher, sondern eher bei extremer Witterung auf, wobei je nach Anwendungsfall ein besonders kaltes (z.B. bei winterlichem Tauwasser) als auch ein besonders warmes Jahr (z.B. bei Sommerkondensation) die ungünstigste Belastung darstellen kann [8].
5.2 Hygrothermische Bedingungen im Erdreich
Im Erdreich setzen sich die Temperaturschwankungen der Außenluft nur sehr gedämpft fort. Bild 6 zeigt den 1 m unter der Erdoberfläche gemessenen Temperaturverlauf für das Jahr 1999 im Vergleich zur Außenlufttemperatur. Die Dämpfung ist in dieser Tiefe bereits so groß, dass keine Tagesgänge mehr feststellbar sind. Außerdem findet eine mehrwöchige Phasenverschiebung zur Lufttemperatur statt, die sich vor allem im Frühjahr und im Herbst bemerkbar macht. Im gemessenen Verlauf sind die Niederschlagseinflüsse (Versickern von Regenwasser, Schneeschmelze, etc.) enthalten. Da die Messungen auf freiem Feld durchgeführt wurden, sind die Temperaturen niedriger als in der Nähe eines Wärme abgebenden Gebäudes. Die Feuchte im Erdreich beträgt in der Regel zwischen 99% und 100% r.F., wenn Vegetation existiert, da Pflanzen nur in diesem Feuchtebereich dem Boden Wasser entziehen können. Dies gilt auch für Substratschichten bei begrünten Dächern, allerdings treten dort andere Temperaturen auf.
5.3 Raumklima
Die in der DIN 4108-3 spezifizierten Raumklimabedingungen für die Tauperiode (20°C, 50% r.F.) und die Verdunstungsperiode (12°C, 70% r.F.) haben sich zwar für die diffusionstechnische Beurteilung von Bauteilen bewährt, sie stellen jedoch keine realistischen Randbedingungen für einen Jahresverlauf dar.
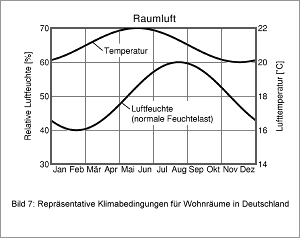
Messungen in Wohnungen [9] zeigen, dass die monatliche Feuchtelast im Raum (Differenz zwischen dem Wassergehalt der Luft innen und außen) fast linear mit der Außenlufttemperatur abnimmt. Das ist auf die stärkere Fensterlüftung in den wärmeren Jahreszeiten zurückzuführen. Die Größe der Feuchtelast im Winter (bei 0°C) bewegt sich je nach Nutzergewohnheiten und Dichtheit des Gebäudes etwa zwischen 2 g/m³ und 6 g/m³. Bei normaler Feuchtelast (4 g/m³) resultiert bei durchschnittlichen deutschen Außenklimaverhältnisse der in Bild 7 dargestellte Verlauf von Raumlufttemperatur und -feuchte. Diese Verläufe sind repräsentativ für die Verhältnisse in Wohnräumen einschließlich Küche und Bad. Sie beinhalten bereits einen gewissen Sicherheitszuschlag vor allem wenn Räume mit geringer Feuchtelast, wie z.B. Büro oder Schlafräume betrachtet werden. Deshalb ist ihr Einsatz zweckmäßig, wenn zum Innenklima keine genaueren Angaben oder Messwerte vorliegen.
5.4 Übergangsbedingungen
Sowohl das Außenklima, mit Ausnahme der Situation im Erdreich, als auch das Raumklima wirken über eine Grenzschicht auf die Bauteiloberfläche ein. Diese Grenzschicht stellt einen strömungsabhängigen Widerstand für den Wärme- und Feuchtetransport dar, der durch entsprechende Übergangskoeffizienten quantifiziert wird. In der Regel ist eine detaillierte Berücksichtigung der spezifischen Konvektionseinflüsse am Bauteil nicht erforderlich, da die Übergangswiderstände im Vergleich zu den Widerständen der einzelnen Materialschichten klein sind. Deshalb sind die in Tabelle 1 aufgelisteten Durchschnittswerte für die äußeren und inneren Wärme- und Feuchteübergangskoeffizienten für die meisten Anwendungsfälle ausreichend.
In den Wärmeübergangskoeffizienten ist ein Anteil enthalten, der den langwelligen Strahlungsaustausch berücksichtigt. Dieser Ansatz ist jedoch nur gültig, solange der konvektive und der strahlungsbedingte Wärmefluss gleichgerichtet sind. Bei der nächtlichen Unterkühlung hochgedämmter Bauteile ist dies nicht mehr der Fall. Für Berechnungen der nächtlichen Betauung solcher Bauteile ist deshalb die explizite Ermittlung und Berücksichtigung der langwelligen Strahlungsbilanz notwendig.

Die Einwirkungen von Sonnenstrahlung und Niederschlag auf das Bauteil lassen sich am besten durch Wärme- und Feuchtequellen beschreiben. Mit Hilfe einer von der Oberflächenfarbgebung abhängigen Energieabsorptionszahl wird der Tatsache Rechnung getragen, dass nur ein Teil der auf das Bauteil auftreffenden kurzwelligen Strahlung in Wärme umgewandelt wird. Diese Absorptionszahl beträgt ca. 0,4 für helle Oberflächen, wie z.B. weiße Außenputze und zwischen 0,6 und 0,8 für dunkle Oberflächen, wie z.B. gestrichenes Holz, Klinker, Dachziegel und Bitumenbahnen.
Auch für die Einwirkung von Schlagregen auf Fassaden ist die Einführung einer Absorptionszahl sinnvoll, da nur ein Teil des ankommenden Regenwassers an der Oberfläche hängen bleibt. Der Rest spritzt beim Auftreffen auf die Fassade wieder weg oder läuft durch die Schwerkraft ab. Die bisherigen Erfahrungen zeigen, dass für den anhaftenden Anteil des Regens auf vertikalen Flächen in der Regel der Wert 0,7 angesetzt werden kann.
6. Rechenverfahren
Auf nationaler und internationaler Ebene gibt es inzwischen mehrere hygrothermische Simulationsverfahren, die zuverlässige Ergebnisse liefern [10]. Die folgende Beschreibung beschränkt sich jedoch auf das Modell, das dem PC-Programm WUFI (Wärme- Und Feuchtetransport Instationär) [2] zugrunde liegt. In diesem Modell werden die zeitlich veränderlichen Wärme- und Feuchtetransportprozesse in Bauteilen mit Hilfe folgender gekoppelter Differentialgleichungen beschrieben:

Beide Gleichungen enthalten auf der linken Seite die Speicherterme. Die Wärmespeicherung setzt sich aus der Wärmekapazität des trockenen Baustoffes und der des darin enthaltenen Wassers zusammen. Die Feuchtespeicherung wird durch die Ableitung der bereits erwähnten Feuchtespeicherfunktion beschrieben.
Auf der rechten Seite der Gleichungen stehen die Transportterme. Der Wärmetransport basiert auf der feuchteabhängigen Wärmeleitung und dem Dampfenthalpiestrom. Dieser Dampfenthalpiestrom transportiert Wärme, indem Wasser an einer Stelle verdunstet und dabei dieser Stelle Wärme entzieht, und anschließend an eine andere Stelle diffundiert, dort kondensiert und dadurch Wärme zuführt. Diese Art des Wärmetransportes wird häufig als Latentwärmeeffekt bezeichnet.
Der Flüssigtransport (durch Oberflächendiffusion und Kapillarleitung, beide infolge eines Gradienten der relativen Feuchte) zeigt nur eine vergleichsweise geringe Temperaturabhängigkeit. Die Dampfdiffusion wird hingegen stark vom Temperaturfeld beeinflusst, da der Sättigungsdampfdruck exponentiell mit der Temperatur ansteigt.
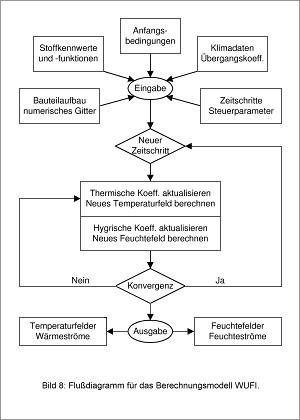
Die Diffentialgleichungen werden mit Hilfe eines impliziten Finite-Volumen-Verfahrens diskretisiert und entsprechend dem Ablaufschema in Bild 8 iterativ gelöst. Die Genauigkeit der numerischen Lösung hängt von der Maschenweite des Gitters, der Größe der Zeitschritte und der Wahl der Abbruchkriterien ab. In der Regel ist die numerische Lösung so genau, dass der Einfluss der numerischen Parameter gegenüber dem Einfluss der physikalischen Parameter, wie Material- und Klimadaten, vernachlässigt werden kann. Nach der Berechnung sollte eine Ergebniskontrolle durchgeführt werden, um Bedienungs- oder schwere Konvergenzfehler ausschließen zu können. Konvergenzprobleme werden von WUFI angezeigt und ihre Auswirkungen anhand eines Vergleichs der aufsummierten Feuchteströme und des akkumulierten Wassers im Bauteil ausgewertet. Falsche Eingaben oder unrealistische Materialdaten können nur durch Plausibilitätskontrollen eingegrenzt werden.
7. Praktische Schlussfolgerungen
Die rechnerische Simulation des instationären Wärme- und Feuchtetransports bietet auch für die Praxis zahlreiche Vorteile. So sind etwa die folgenden Einsatzbereiche und Aussagemöglichkeiten in Bezug auf das klimabedingte hygrothermische Bauteilverhalten zu nennen, die über die bisherigen Beurteilungsmöglichkeiten nach Glaser deutlich hinausgehen:
Die Ergebnisse für Feuchte und Temperatur im Bauteil sind in beliebiger Orts- und Zeitauflösung verfügbar. Sie können beispielsweise verwendet werden zur:
Die aufgezeigten Vorteile der hygrothermischen Simulation haben in den letzten Jahren zu einer starken Nachfrage nach rechnerischen Untersuchungen vor allem im Bereich der Altbausanierung geführt, da dort Standardlösungen häufig versagen. Bisher fehlen jedoch allgemeingültige Richtlinien für die Leistungsbeschreibung und Anwendung der neuen Verfahren. Deshalb wurde 1997 auf Initiative der WTA (Wissenschaftlich-Technische Arbeitsgemeinschaft für Bauwerkserhaltung und Denkmalpflege) eine WTA-Arbeitsgruppe gebildet, die die Erstellung solcher Richtlinien zur Aufgabe hat. Ein ähnliches Ziel verfolgt die im Jahr 2000 gegründete Task Group "Moisture Calculation" im Rahmen des europäischen Normungsausschusses TC89 (Thermal Performance of Buildings and Building Components). Damit werden sowohl auf nationaler als auch auf internationaler Ebene die Voraussetzungen für den geregelten Einsatz von hygrothermischen Simulationsverfahren im Bauwesen geschaffen.
Literatur
[ 1] Cammerer, J. und Achtziger,J.: Einfluß des Feuchtegehaltes auf die Wärmeleitfähigkeit von Bau- und Dämmstoffen. Bericht zu BmBau Forschungsvorhaben BI 5-800883-4, 1984.
[ 2] Künzel H.M.: Verfahren zur ein- und zweidimensionalen Berechnung des gekoppelten Wärme- und Feuchtetransports in Bauteilen mit einfachen Kennwerten; Dissertation Universität Stuttgart 1994.
[ 3] Künzel, H.M. und Holm, A.: Praktische Beurteilung von Putzen durch moderne bauphysikalische Bewertung. WTA-Schriftenreihe (1999), Heft 20, S.177-132.
[ 4] Arnold, A.: Salze, lästige weiße Ausblühungen oder Hauptschadensursache. Jahresbericht Steinzerfall-Steinkonservierung 1990, Verlag Ernst & Sohn, S. 1-9.
[ 5] Sedlbauer, K. und Krus, M.: Schadensrisiko bei Ziegel-Außenbauteilen durch Niederschlag und Frosteinwirkung. Feuchtetag 1999 DGZfP-Berichtsband BB 69-CD, Vortrag U4, S.1-8.
[ 6] Krus, M.: Feuchtetransport- und Speicherkoeffizienten poröser mineralischer Baustoffe. Theoretische Grundlagen und neue Meßtechniken. Dissertation Universität Stuttgart 1995.
[ 7] Künzel, H.M.: Einfluß der Mittelwertbildung von Klimadaten auf die Ergebnisse von Feuchtetransportberechnungen. Tagungsband 9. Bauklimatisches Symposium, Dresden 1994, S. 332-344.
[ 8] Künzel, H.M. und Schmidt, Th.: Auswahl und Aufbereitung von meteorologischen Datensätzen für Feuchtetransportberechnungen. Tagungs-band 10. Bauklimatisches Symposium, Dresden 1999, S. 637-647.
[ 9] Künzel, H.M.: Raumluftfeuchteverhältnisse in Wohnräumen. IBP-Mitteilung 24 (1997) Nr. 314.
[10] Hens, H.: Modelling Heat Air and Moisture Transfer in Insulated Envelope Parts. Final Report IEA-Annex 24, KU Leuven 1996.
Rechnerische Simulation mit Hilfe des Modells WUFI
1. Einleitung
Beim Thema "Feuchtetransport durch Bauteile" denkt der Praktiker in erster Linie an Dampfdiffusion, Taupunkt und das Glaser-Verfahren in der DIN 4108. Wird ein Bauteil "nach Glaser" als unbedenklich eingestuft, so ist in der Regel damit für den Planer alles erledigt.
Erst wenn dennoch unerwartet Feuchteschäden auftreten, oder das geplante Bauteil bei der Normberechnung nach Glaser durchfällt, wird nach alternativen Beurteilungsmöglichkeiten gesucht. Da die winterliche Tauwasserbildung durch Dampfdiffusion (ausschließlich damit befasst sich Glaser) nur eine Feuchtebelastung unter vielen darstellt, kann eine positive Bewertung nach DIN 4108 eine Feuchtesicherheit vortäuschen, die gar nicht vorhanden ist. Probleme mit anderen Feuchteeinwirkungen, wie z.B. durch Raumluftkonvektion, Niederschlag oder aufsteigende Feuchte sind hierbei nicht berücksichtigt. Das gleiche gilt für die Baufeuchte, die beim heutigen Termindruck auf den Baustellen eine zunehmende Brisanz erfährt.
Um auch diese Einflüsse erfassen zu können, muss von dem einfachen stationären Bewertungsverfahren nach Glaser zur realitätsnahen Simulation der Feuchteverhältnisse in Bauteilen übergegangen werden. Zu diesem Zweck sind in den letzten Jahren neue instationäre Rechenverfahren entwickelt und experimentell validiert worden, deren Zuverlässigkeit inzwischen so groß ist, dass sich ihr Einsatz auch in der Praxis immer mehr durchsetzt. Dieser Tatsache wird auch in der Neufassung der DIN 4108 Teil 3 durch entsprechende Hinweise Rechnung getragen.
Im Folgenden werden die Auswirkungen von erhöhter Feuchte und von Feuchtewechselbeanspruchungen in Bauteilen aufgezeigt und die physikalischen Grundlagen des Feuchteverhaltens von Bauteilen beschrieben. Anhand des inzwischen weit verbreiteten instationären Simulationsmodells WUFI werden anschließend die Voraussetzungen in bezug auf die Material- und Klimadaten sowie die Genauigkeit der Berechnungen analysiert.
2. Feuchtewirkungen in Bauteilen
Die Gebrauchstauglichkeit und die Dauerhaftigkeit von Bauteilen und Baustoffen kann durch Feuchteeinwirkungen beeinträchtigt werden, z.B.:
- Verminderung der Wärmedämmung
- verstärkte Verschmutzung, Algen- oder Schimmelpilzbildung
- mechanische Belastung bei Quell- und Schwindvorgängen durch Feuchtewechsel sowie bei Salzkristallisationsprozessen
- Schäden durch Frost, Fäulnis oder Korrosion bei erhöhter Materialfeuchte
- unvollständige Hydratation durch zu rasche Trocknung
- verzögerte Estrichbelegreife durch zu langsame Trocknung
2.1 Feuchtebedingte Wärmeverluste
In der Regel sind die Wärme- und Feuchtetransportprozesse in Gebäuden stark gekoppelt. Dies zeigt sich besonders deutlich beim Feuchteeinfluss auf die Wärmedämmung von Bauteilen. Bild 1 zeigt den Anstieg der Wärmeleitfähigkeit von drei verschiedenen Baustoffen in Abhängigkeit vom Wassergehalt nach [1].

Während die Wärmeleitung mineralischer Wandbildner, wie bei dem hier dargestellten Porenbeton, linear mit dem Wassergehalt ansteigt, ist der Anstieg bei Polystyrol-Hartschaum leicht progressiv.
Überraschend ist der starke Anstieg der Wärmeleitfähigkeit von Mineralwolle schon bei sehr kleinem Wassergehalt. Dies ist auf die starke Feuchteverlagerung durch Dampfdiffusion nach Anlegen eines Temperaturgradienten in der Mineralwolle zurückzuführen. Hier handelt es sich um so genannte instationäre Latentwärmeeffekte, bedingt durch die Phasenwechsel der Materialfeuchte während der Messung im Plattenapparat. Diese Latentwärmeeffekte sind in der Regel kurzfristiger Natur und haben nichts mit der realen Wärmeleitfähigkeit des Dämmstoffes zu tun. Da ihr Einfluss stark von den an die Wärmedämmung angrenzenden Bauteilschichten abhängt, können sie nicht dem Dämmstoff selbst zugeordnet werden [2].
Die Darstellung der Wärmeleitfähigkeit für die Mineralwolle in Bild 1 ist daher als Stoffeigenschaftsfunktion sowohl für instationäre Berechnungen als auch für die Ermittlung des stationären Wärmedurchgangskoeffizienten (U-Wert; früher k-Wert) wenig geeignet. Durch entsprechende Vorkehrungen bei der Messung im Plattenapparat lässt sich jedoch die echte Wärmeleitfähigkeit der Mineralwolle ermitteln. Ergebnisse aus solchen Untersuchungen belegen, dass die Wärmeleitfähigkeit der Mineralwolle ohne Latentwärmeeffekte eine ganz ähnliche Feuchteabhängigkeit zeigt, wie die von Polystyrol-Hartschaum in Bild 1. Ähnliches gilt auch für andere diffusionsoffene Dämmstoffe.
2.2 Mechanische Beanspruchung durch hygrothermische Wechsellast
Ein Beispiel für den stark instationären Charakter der gekoppelten Temperatur- und Feuchtewirkungen sind die mechanischen Belastungen durch thermische und hygrische Verformungen bzw. die daraus resultierenden Eigenspannungen in Außenputzen auf Wärmedämmverbundsystemen. Im Tagesverlauf sind diese Putzoberflächen Temperatur- und Feuchteschwankungen von bis zu 40 K und 80 % r.F. ausgesetzt [3].

Bild 2 zeigt den Vergleich zwischen thermischer und hygrischer Längenänderung von solchen Außenputzen. Die abgebildeten Werte stellen den Durchschnitt aus Labormessungen an über 20 Proben unterschiedlicher Hersteller dar. Übertragen auf die Verhältnisse am Bau würde dies bei freier Verformbarkeit der Außenputze eine thermisch bedingte Längenänderung von 0,4 mm/m und eine noch größere hygrische Dilatation von 0,7 mm/m bedeuten. Beide Prozesse sind jedoch häufig gegenläufig, da der Putz bei einer Erhöhung der Temperatur austrocknet, was die thermisch bedingte Ausdehnung mit einer gewissen Zeitverzögerung durch hygrisches Schwinden kompensiert. Da die Putzoberflächen jedoch in der Regel nicht frei beweglich sind, kommt es zu Spannungen und bei Überschreiten der Festigkeit zu Rissen oder Ablösungen vom Untergrund.
Weitere Beispiele für Bauschäden aufgrund von hygrothermischen Wechselbeanspruchungen sind Salz- und Frostschäden. Salze kristallisieren unterhalb einer für die Salzart typischen relativen Feuchte aus der Lösung. Wird umgekehrt dieser Kristallisationspunkt wieder überschritten, ziehen sie Wasserdampf aus der Umgebung an und gehen wieder in Lösung. Diese Vorgänge finden auch in den Porenräumen von salzhaltigen Baustoffen statt. Da die Kristallisation dort jedoch durch das enge Porengefüge behindert wird, können erhebliche Kristallisationsdrücke entstehen, die bei einem häufigen Feuchtewechsel zum Zermürben des Materials führen. Je nach Löslichkeit des Salzes spielt sich dieser Prozess an der Oberfläche oder einige Millimeter bis Zentimeter darunter ab und führt entweder zu einem oberflächlichen Absanden der Bausubstanz oder zur Schalenbildung durch Entfestigung der tiefer liegenden Schichten [4]. Frost kann ganz ähnliche Schadensbilder erzeugen, wobei in diesem Fall die Eiskristalle die Rolle der Salzkristalle übernehmen. Ausschlaggebend sind hier die Temperaturwechsel um den Gefrierpunkt und der Wassergehalt in der Frostzone [5].
Die vorangegangenen Beispiele zeigen die Bedeutung von hygrothermischen Wechselbeanspruchungen für die Gebrauchstauglichkeit und die Dauerhaftigkeit von Baustoffen und Bauteilen. Eine genaue Erfassung der wärme- und feuchtetechnischen Prozesse in Baustoffen und Bauteilen ist deshalb nicht nur wünschenswert sondern dringend erforderlich. Beurteilungen mit den bisher eingeführten, ausschließlich auf der Dampfdiffusion basierenden Berechnungsmethoden, wie z.B. dem Glaser-Verfahren, sind hierfür nur in Ausnahmefällen geeignet. Die rechnerische Simulation des instationären Temperatur- und Feuchteverhaltens unter Berücksichtigung aller wesentlichen Transportmechanismen bei natürlichen Klimabedingungen ist inzwischen jedoch so weit entwickelt und auch in der Praxis erprobt, dass ihre konsequente Anwendung in vielen Bereichen des Hochbaus sinnvoll erscheint. Unter diesem Gesichtspunkt sind die folgenden Ausführungen primär zu verstehen.
3. Feuchtespeicher- und Feuchtetransportmechanismen
Für die Anwendung von Simulationsverfahren zur instationären Berechnung des Wärme- und Feuchteverhaltens von Bauteilen sind Grundkenntnisse in bezug auf die Speicher- und Transporteigenschaften von Baustoffen notwendig. Da die Wärmespeicherung und die Wärmeleitung hinlänglich bekannt sind und der Wärmetransport durch Dampfdiffusion mit Phasenwechsel (Latentwärmeeffekt) im Zusammenhang mit dem Feuchtetransport zu sehen ist, wird hier ausschließlich auf die Feuchtephänomene eingegangen. Für die genauere Analyse von Frost-Tau-Prozessen, bei denen die Schmelzwärme und die wärmetechnischen Eigenschaften des Eises eine Rolle spielen, wird auf die Erläuterungen in [2] verwiesen.
3.1 Feuchtespeicherung
Man unterscheidet hygroskopische und nicht hygroskopische Baustoffe. Ist ein Baustoff hygroskopisch, dann nimmt er vom trockenen Zustand aus solange Wasserdampf aus der Luft auf, bis er seine Ausgleichsfeuchte bei den jeweiligen Umgebungsbedingungen erreicht hat. Da die Wasserdampfsorption in erster Linie von der umgebenden relativen Luftfeuchte abhängt, während die Umgebungstemperatur einen demgegenüber geringeren Einfluss hat, wird die hygroskopische Feuchtespeicherung in Form von stoffspezifischen Sorptionskurven dargestellt.

Bild 3 zeigt die Verläufe solcher Sorptionskurven (auch Sorptionsisothermen genannt) für drei in ihrer Hygroskopizität sehr unterschiedliche Baustoffe. Die Sorptionsisothermen werden durch Lagerung der Baustoffproben bei verschiedenen Umgebungsbedingungen im Labor bestimmt. Die obere Grenze des Messbereichs liegt bei etwa 95% r.F., da eine höhere Luftfeuchte wegen der Regelungscharakteristika der meisten Klimakammern zur Betauung der Proben führen würde.
Darüber hinaus bis zur freien Wassersättigung im sog. überhygroskopischen Bereich muss deshalb auf die in [6] beschriebene Saugspannungsmessung zurückgegriffen werden. Bei dieser Messmethode werden Baustoffproben zunächst durch Wasserlagerung frei (d.h. drucklos) gesättigt. Anschließend wird das Wasser in mehreren Druckstufen bis max. 100 bar entfernt, wobei sich bei jeder Druckstufe ein Gleichgewichtswassergehalt einstellt. Die Auswertung dieser Messung ergibt eine überhygroskopische Feuchtespeicherfunktion (dargestellt im blau hinterlegten Bereich in Bild 3), die nahtlos an die klassische Sorptionsisotherme anschließt. Bei grobporigen mineralischen Baustoffen wie z.B. Ziegel ist der überhygroskopische Wassergehaltsbereich größer als der hygroskopische, so dass für genaue Analysen auf Saugspannungsmessungen nicht verzichtet werden kann. Bei feinporigen Materialien wie z.B. Beton ist die Sorptionsfeuchte bei 93% r.F. bereits so hoch, dass der Verlauf im überhygroskopischen Bereich bis zur freien Wassersättigung ohne Genauigkeitsverlust extrapolierbar ist. Holz und Holzwerkstoffe sorbieren ebenfalls schon im hygroskopischen Bereich große Feuchtemengen, so dass auch dort eine Extrapolation bis zur freien Wassersättigung in der Regel ausreicht.
Bei nicht hygroskopischen Baustoffen, wie z.B. Glas, Metall oder einigen Schaumkunststoffen, lagert sich ohne Taupunktsunterschreitung kein Wasser ein. Sie trocknen bei Umgebungsbedingungen unter 100% relativer Feuchte vollständig aus.
3.2 Feuchtetransport
Der Feuchtetransport erfolgt in porösen Baustoffen im Wesentlichen durch Dampfdiffusion, Oberflächendiffusion und Kapillarleitung. In Baustoffen, die kein starres Porengefüge besitzen, wie z.B. Kunststoffe, findet aufgrund der Einlagerung von Wassermolekülen zwischen die polymeren Makromoleküle die so genannte Lösungsdiffusion statt. Bisherige Erfahrungen zeigen, dass diese Art der Diffusion am ehesten durch den Dampfdiffusionsansatz beschreibbar ist, wobei der Diffusionswiderstand im Gegensatz zur normalen Dampfdiffusion von der Umgebungsfeuchte abhängt.
Andere Transportphänomene, wie z.B. Sickerströmung durch Gravitation im nicht wassergesättigten Porenraum oder Wanderung von Wassermolekülen durch elektrische Felder oder osmotische Drücke sind bislang nur unzureichend berechenbar. Da sie nur in Ausnahmefällen eine Rolle spielen, werden sie hier nicht betrachtet. Ebenfalls nicht berücksichtigt werden Konvektionsvorgänge, wie z.B. das Durchströmen von Bauteilen mit feuchter Raumluft aufgrund von Luftdruckunterschieden zwischen innen und außen. Da die Luftdichtheit eine zentrale Anforderung an die Gebäudehülle darstellt, findet die Luftkonvektion in der Praxis ausschließlich unplanmäßig durch Fehlstellen oder ungeeignete Bauteilschichten statt. Sie ist deshalb kaum vorab quantifizierbar und ließe sich auch nur durch dreidimensionale strömungsmechanische Simulationsprogramme in realistischer Weise erfassen. (Das Luftinfiltrationsmodell in WUFI erlaubt eine stark vereinfachte Berücksichtigung von Undichtheiten)
Das Zusammenspiel der oben genannten dominierenden Feuchtetransportphänomene wird in Bild 4 anhand einer Zylinderkapillare in einem Wandausschnitt erläutert. Auf beiden Seiten der betrachteten Kapillare sollen bauübliche Randbedingungen herrschen, d.h. der Dampfdruck sei innen größer als außen und die relative Luftfeuchte sei außen höher als innen. Ist der Baustoff ausreichend trocken oder nicht hygroskopisch, dann diffundiert der Wasserdampf entsprechend dem Dampfdruckgefälle von innen nach außen.

Enthält der Baustoff genügend hygroskopische Feuchte, so dass der Sorbatfilm an den Porenwandungen beweglich wird (dies ist etwa ab 60% r.F. der Fall), dann findet neben der normalen Dampfdiffusion auch die so genannte Oberflächendiffusion durch sorbiertes Wasser an den Porenwandungen statt. Da die Dicke und damit Beweglichkeit der sorbierten Molekülschicht mit der relativen Feuchte zunimmt, erfolgt wie in [6] nachgewiesen ein Feuchtetransport im Sorbatfilm entgegen dem Dampfdruckgefälle von Bereichen höherer Konzentration in Bereiche mit geringerer Konzentration an sorbiertem Wasser. Die treibende Kraft für die Oberflächendiffusion ist daher die relative Feuchte und nicht der Dampfdruck. Unter den hier angenommenen Randbedingungen verlaufen Dampfdiffusion und Oberflächendiffusion in entgegengesetzte Richtungen. Bei der Oberflächendiffusion handelt es sich also um einen Flüssigtransport und nicht um eine Dampfdiffusion in der Gasphase. Dennoch ist es häufig zweckmäßig, die Oberflächendiffusion der Dampfdiffusion zuzuschlagen, z.B. durch Verwendung des im Feuchtbereich (wet-cup) nach DIN 52615 ermittelten µ-Wertes. Dieses Vorgehen führt zu ähnlichen Rechenergebnissen wie die strikte Trennung beider Transportphänomene, wenn in der betrachteten Bauteilschicht keine großen Temperaturgradienten auftreten.
Bei überhygroskopischer Feuchte im Material, beispielsweise infolge von Schlagregen, kommt es bei Füllung der Poren zur so genannten Kapillarleitung, die die effizienteste Form des Feuchtetransports darstellt. Die treibende Kraft ist hier der kapillare Unterdruck, der sich aufgrund der Oberflächenspannung des Wassers im Meniskus an der Grenzfläche zwischen Porenluft und Wasser bildet. Der kapillare Unterdruck steht in einem funktionalen Zusammenhang mit der relativen Feuchte der Porenluft über dem Meniskus, d.h. der treibenden Kraft in der flüssigen Phase kann eine bestimmte relative Luftfeuchte in der Gasphase zugeordnet werden. Alternativ zum kapillaren Unterdruck kann deshalb auch die relative Feuchte als Transportpotential für die Kapillarleitung verwendet werden.
Das Beispiel zeigt deutlich die häufig entgegengesetzten Transportrichtungen von Dampfdiffusion und Flüssigtransport. Die Dampfdiffusion erfolgt meist von warm nach kalt, während der Flüssigtransport weitgehend temperaturunabhängig von feucht nach trocken gerichtet ist. Dieses Phänomen, das jedem Praktiker von der kapillaren Rückleitung (auch kapillare Entspannung genannt) in mineralische Baustoffe bei winterlicher Tauwasserbildung bekannt sein dürfte, muss auch in einem Berechnungsmodell entsprechend der vorangegangenen Analyse korrekt erfasst werden. Das bedeutet, dass für Dampfdiffusion und Flüssigtransport unterschiedliche Triebkräfte angesetzt werden müssen. Besonders vorteilhaft erweist sich in diesem Zusammenhang die Wahl von Temperatur und relativer Feuchte als Transportpotentiale. Der Dampfdruck als treibende Kraft für die Diffusion ist durch beide Größen eindeutig bestimmt. Beide Potentiale sind über den Bauteilquerschnitt stetig, d.h. es treten keine Sprünge an den Materialgrenzen auf, wie das beispielsweise beim Wassergehalt der Fall ist. Auch die im folgenden beschriebenen hygrothermischen Stoffkennwerte und die Randbedingungen lassen sich mit ihrer Hilfe auf einfache Weise definieren.
4. Hygrothermische Stoffkennwerte
Die Ergebnisse einer rechnerischen Simulation sind immer nur so gut wie die zugrunde gelegten Materialparameter. Nachdem der Mangel an zuverlässigen Stoffkennwerten lange Zeit die Akzeptanz moderner Rechenverfahren behindert hat, soll hier gezeigt werden, welche Parameter für die verschiedenen Fragestellungen wirklich notwendig sind. In der Regel sind für die instationäre Berechnung der Temperaturfelder folgende Stoffkennwerte erforderlich:
- Trockenrohdichte rho
- spezifische Wärmekapazität c
- Wärmeleitfähigkeit lambda
Falls der Einfluss der Materialfeuchte auf den Wärmedurchgangskoeffizienten (U-Wert) quantifiziert werden soll, muss die Wärmeleitfähigkeit, wie in Bild 1 gezeigt, als Funktion des Wassergehalts eingegeben werden. Angaben dazu finden sich in [1] bzw. in der WUFI-Materialdatenbank. Liegt das Hauptaugenmerk auf dem Feuchteverhalten des Bauteils, dann reicht die Eingabe des Rechenwertes lambda_R, der den praktischen Feuchtegehalt des jeweiligen Baustoffes schon enthält. Das heißt, im Normalfall können alle notwendigen thermischen Stoffkennwerten der DIN 4108-4 oder den entsprechenden Baustoffzulassungen entnommen werden.
Die feuchtetechnischen Kennwerte, die für alle Baustoffe, also auch für nicht hygroskopische Materialien, vorhanden sein müssen, sind:
- Wasserdampfdiffusionswiderstandszahl µ (µ-Wert)
- Porosität epsilon (als Maß für den maximal möglichen Wassergehalt wmax)
Die µ-Werte für eine große Anzahl von Baustoffen sind ebenfalls in der DIN 4108-4 enthalten. Die Porosität kann aus Rohdichte und Reindichte oder aus der maximalen Wassersättigung ermittelt werden. Sie spielt allerdings nur dann eine Rolle, wenn der Baustoff Wasser oder Wasserdampf in sein Porengefüge aufnehmen kann. Mit den bisher genannten Materialdaten ist jedoch lediglich eine Art instationäre Glaser-Berechnung möglich, weil noch kein Feuchtespeichervermögen und keine Flüssigtransportvorgänge berücksichtigt sind.
Soll das Verhalten von hygroskopischen, kapillaraktiven Baustoffen korrekt erfasst werden, sind außerdem noch die bereits in Bild 3 gezeigte Feuchtespeicherfunktion und die in Bild 5 dargestellten feuchteabhängigen Flüssigtransportkoeffizienten erforderlich. Bei diesen Koeffizienten hat sich die im Bild gezeigte prozessabhängige Differenzierung als vorteilhaft erwiesen. Das hängt damit zusammen, dass der Befeuchtungsvorgang von mineralischen Baustoffen in Kontakt mit Wasser deutlich schneller abläuft als die kapillare Weiterverteilung bzw. Trocknung nach Unterbrechung der Wasserzufuhr.

Diese zusätzlichen Parameter zur Beschreibung der hygroskopischen und kapillaren Eigenschaften sind inzwischen für zahlreiche Baustoffe in einschlägigen Datenbanken (z.B. WUFI-Datenbank) vorhanden. Die messtechnische Bestimmung von Feuchtespeicherfunktion und Flüssigtransportkoeffizienten ist etwas aufwändig [6], so dass sie für den Praktiker im Normalfall nicht in Frage kommt.
In vielen Fällen können jedoch Näherungsverfahren eingesetzt werden, um diese Kenndaten aus anderen, bekannten Kenndaten abzuleiten. Sind z.B. die kapillaraktiven Materialschichten in einem Bauteil nicht in direktem Kontakt, oder wird diese Kontaktschicht nicht langfristig nass (d.h. findet kein merklicher kapillarer Feuchteaustausch über die Kontaktschicht statt), dann werden mit Hilfe der in WUFI [2] implementierten Approximationsmöglichkeit für die Feuchtespeicherfunktion aus dem Bezugsfeuchtegehalt u80 (Gleichgewichtsfeuchte bei 80% r.F.) gemäß DIN 52620 und der freien Wassersättigung uf ausreichend genaue Rechenergebnisse erzielt.
Ähnliches gilt für die ebenfalls in WUFI integrierte Approximation der Flüssigtransportkoeffizienten (Bild 5) aus dem Wasseraufnahmekoeffizienten (w-Wert) nach DIN 52617.
Für die meisten praktischen Anwendungen können also hygroskopische und kapillaraktive Baustoffe durch folgende - über die Standardstoffkennwerte in DIN 4108-4 hinausgehende - Materialparameter ausreichend genau spezifiziert werden:
- Bezugsfeuchtegehalt u80
- freie Wassersättigung uf
- Wasseraufnahmekoeffizient w (w-Wert)
Die freie Wassersättigung ist der Wassergehalt, der bei der w-Wert-Messung im Zustand der Durchfeuchtung bestimmt wird.
Da alle Materialeigenschaften von Baustoffen herstellungs- oder verarbeitungsbedingten Schwankungen unterworfen sind, ist es zweckmäßig, die Stoffkennwerte bei der Berechnung analog zu den Vorgaben in der DIN 4108-4 in bestimmten Grenzen zu variieren und den Einfluss dieser Variation auf die Rechenergebnisse zu dokumentieren. Stellt sich der Einfluss eines Materialparameters im betrachteten Anwendungsfall als gering heraus, dann erübrigt sich eine exakte Bestimmung von selbst. Hat der Einfluss des jeweiligen Kennwertes jedoch eine entscheidende Bedeutung für die Interpretation der Ergebnisse, sind Norm- oder Literaturdaten weniger geeignet. Hier sind genaue Messungen der entsprechenden Stoffeigenschaften vorzuziehen.
5. Klima- und Übergangsbedingungen
Jedes Bauteil steht über seine Oberflächen in hygrothermischer Wechselwirkung mit der Umgebung. Das heißt, dass nicht nur die Umgebung auf das Bauteil einwirkt, sondern umgekehrt auch das Bauteil auf die Umgebung, wie z.B. durch Abgabe von gespeicherter Wärme oder durch sorptive Pufferung von Raumluftfeuchte. Diese Tatsache ist bei der Formulierung der Randbedingungen zu beachten.
Grundsätzlich sind drei Bereiche zu unterscheiden: die äußeren Umgebungsbedingungen über sowie unter der Geländeoberkante und die Innenraumverhältnisse. In allen drei Fällen sind, bedingt durch die jeweiligen Austauschprozesse mittels Konvektion und Strahlung bzw. Leitung und Diffusion, unterschiedliche Oberflächenübergangsbedingungen anzusetzen.
5.1 Außenklima
Die auf ein Bauteil einwirkenden Außenklimabedingungen sind die Lufttemperatur, die Luftfeuchte, sowie die Sonnenstrahlung und der Niederschlag. Die Strahlungs- und Niederschlagsbelastung ist abhängig von der Neigung und Orientierung des Bauteils und muss auf die vorliegenden Verhältnisse umgerechnet werden. Zur Ermittlung des Schlagregens sind zusätzlich Windgeschwindigkeit und Windrichtung sowie Kenntnisse der Gebäudeumströmungsverhältnisse erforderlich. Soll die langwellige Abstrahlung berücksichtigt werden, müssen auch Daten zur terrestrischen und atmosphärischen Gegenstrahlung vorliegen.

Die täglichen Schwankungen der Witterungsverhältnisse, dargestellt am Beispiel der Lufttemperatur in Bild 6, erfordern in der Regel kurzfristige Betrachtungsintervalle. Für hygrothermische Simulationsrechnungen hat sich der Einsatz von Stundenmittelwerten als günstig erwiesen [7]. Dafür stehen beispielsweise Test-Referenzjahre TRY des Deutschen Wetterdienstes (ohne Regen) oder Hygrothermische Referenzjahre HRY des IBP (mit Regen) zur Verfügung, die jeweils typische Klimabedingungen für entsprechend eingeteilte Klimaregionen der Bundesrepublik beinhalten. Feuchteprobleme treten jedoch in der Regel nicht bei durchschnittlicher, sondern eher bei extremer Witterung auf, wobei je nach Anwendungsfall ein besonders kaltes (z.B. bei winterlichem Tauwasser) als auch ein besonders warmes Jahr (z.B. bei Sommerkondensation) die ungünstigste Belastung darstellen kann [8].
5.2 Hygrothermische Bedingungen im Erdreich
Im Erdreich setzen sich die Temperaturschwankungen der Außenluft nur sehr gedämpft fort. Bild 6 zeigt den 1 m unter der Erdoberfläche gemessenen Temperaturverlauf für das Jahr 1999 im Vergleich zur Außenlufttemperatur. Die Dämpfung ist in dieser Tiefe bereits so groß, dass keine Tagesgänge mehr feststellbar sind. Außerdem findet eine mehrwöchige Phasenverschiebung zur Lufttemperatur statt, die sich vor allem im Frühjahr und im Herbst bemerkbar macht. Im gemessenen Verlauf sind die Niederschlagseinflüsse (Versickern von Regenwasser, Schneeschmelze, etc.) enthalten. Da die Messungen auf freiem Feld durchgeführt wurden, sind die Temperaturen niedriger als in der Nähe eines Wärme abgebenden Gebäudes. Die Feuchte im Erdreich beträgt in der Regel zwischen 99% und 100% r.F., wenn Vegetation existiert, da Pflanzen nur in diesem Feuchtebereich dem Boden Wasser entziehen können. Dies gilt auch für Substratschichten bei begrünten Dächern, allerdings treten dort andere Temperaturen auf.
5.3 Raumklima
Die in der DIN 4108-3 spezifizierten Raumklimabedingungen für die Tauperiode (20°C, 50% r.F.) und die Verdunstungsperiode (12°C, 70% r.F.) haben sich zwar für die diffusionstechnische Beurteilung von Bauteilen bewährt, sie stellen jedoch keine realistischen Randbedingungen für einen Jahresverlauf dar.
Messungen in Wohnungen [9] zeigen, dass die monatliche Feuchtelast im Raum (Differenz zwischen dem Wassergehalt der Luft innen und außen) fast linear mit der Außenlufttemperatur abnimmt. Das ist auf die stärkere Fensterlüftung in den wärmeren Jahreszeiten zurückzuführen. Die Größe der Feuchtelast im Winter (bei 0°C) bewegt sich je nach Nutzergewohnheiten und Dichtheit des Gebäudes etwa zwischen 2 g/m³ und 6 g/m³. Bei normaler Feuchtelast (4 g/m³) resultiert bei durchschnittlichen deutschen Außenklimaverhältnisse der in Bild 7 dargestellte Verlauf von Raumlufttemperatur und -feuchte. Diese Verläufe sind repräsentativ für die Verhältnisse in Wohnräumen einschließlich Küche und Bad. Sie beinhalten bereits einen gewissen Sicherheitszuschlag vor allem wenn Räume mit geringer Feuchtelast, wie z.B. Büro oder Schlafräume betrachtet werden. Deshalb ist ihr Einsatz zweckmäßig, wenn zum Innenklima keine genaueren Angaben oder Messwerte vorliegen.

5.4 Übergangsbedingungen
Sowohl das Außenklima, mit Ausnahme der Situation im Erdreich, als auch das Raumklima wirken über eine Grenzschicht auf die Bauteiloberfläche ein. Diese Grenzschicht stellt einen strömungsabhängigen Widerstand für den Wärme- und Feuchtetransport dar, der durch entsprechende Übergangskoeffizienten quantifiziert wird. In der Regel ist eine detaillierte Berücksichtigung der spezifischen Konvektionseinflüsse am Bauteil nicht erforderlich, da die Übergangswiderstände im Vergleich zu den Widerständen der einzelnen Materialschichten klein sind. Deshalb sind die in Tabelle 1 aufgelisteten Durchschnittswerte für die äußeren und inneren Wärme- und Feuchteübergangskoeffizienten für die meisten Anwendungsfälle ausreichend.
In den Wärmeübergangskoeffizienten ist ein Anteil enthalten, der den langwelligen Strahlungsaustausch berücksichtigt. Dieser Ansatz ist jedoch nur gültig, solange der konvektive und der strahlungsbedingte Wärmefluss gleichgerichtet sind. Bei der nächtlichen Unterkühlung hochgedämmter Bauteile ist dies nicht mehr der Fall. Für Berechnungen der nächtlichen Betauung solcher Bauteile ist deshalb die explizite Ermittlung und Berücksichtigung der langwelligen Strahlungsbilanz notwendig.

Die Einwirkungen von Sonnenstrahlung und Niederschlag auf das Bauteil lassen sich am besten durch Wärme- und Feuchtequellen beschreiben. Mit Hilfe einer von der Oberflächenfarbgebung abhängigen Energieabsorptionszahl wird der Tatsache Rechnung getragen, dass nur ein Teil der auf das Bauteil auftreffenden kurzwelligen Strahlung in Wärme umgewandelt wird. Diese Absorptionszahl beträgt ca. 0,4 für helle Oberflächen, wie z.B. weiße Außenputze und zwischen 0,6 und 0,8 für dunkle Oberflächen, wie z.B. gestrichenes Holz, Klinker, Dachziegel und Bitumenbahnen.
Auch für die Einwirkung von Schlagregen auf Fassaden ist die Einführung einer Absorptionszahl sinnvoll, da nur ein Teil des ankommenden Regenwassers an der Oberfläche hängen bleibt. Der Rest spritzt beim Auftreffen auf die Fassade wieder weg oder läuft durch die Schwerkraft ab. Die bisherigen Erfahrungen zeigen, dass für den anhaftenden Anteil des Regens auf vertikalen Flächen in der Regel der Wert 0,7 angesetzt werden kann.
6. Rechenverfahren
Auf nationaler und internationaler Ebene gibt es inzwischen mehrere hygrothermische Simulationsverfahren, die zuverlässige Ergebnisse liefern [10]. Die folgende Beschreibung beschränkt sich jedoch auf das Modell, das dem PC-Programm WUFI (Wärme- Und Feuchtetransport Instationär) [2] zugrunde liegt. In diesem Modell werden die zeitlich veränderlichen Wärme- und Feuchtetransportprozesse in Bauteilen mit Hilfe folgender gekoppelter Differentialgleichungen beschrieben:

Beide Gleichungen enthalten auf der linken Seite die Speicherterme. Die Wärmespeicherung setzt sich aus der Wärmekapazität des trockenen Baustoffes und der des darin enthaltenen Wassers zusammen. Die Feuchtespeicherung wird durch die Ableitung der bereits erwähnten Feuchtespeicherfunktion beschrieben.
Auf der rechten Seite der Gleichungen stehen die Transportterme. Der Wärmetransport basiert auf der feuchteabhängigen Wärmeleitung und dem Dampfenthalpiestrom. Dieser Dampfenthalpiestrom transportiert Wärme, indem Wasser an einer Stelle verdunstet und dabei dieser Stelle Wärme entzieht, und anschließend an eine andere Stelle diffundiert, dort kondensiert und dadurch Wärme zuführt. Diese Art des Wärmetransportes wird häufig als Latentwärmeeffekt bezeichnet.
Der Flüssigtransport (durch Oberflächendiffusion und Kapillarleitung, beide infolge eines Gradienten der relativen Feuchte) zeigt nur eine vergleichsweise geringe Temperaturabhängigkeit. Die Dampfdiffusion wird hingegen stark vom Temperaturfeld beeinflusst, da der Sättigungsdampfdruck exponentiell mit der Temperatur ansteigt.

Die Diffentialgleichungen werden mit Hilfe eines impliziten Finite-Volumen-Verfahrens diskretisiert und entsprechend dem Ablaufschema in Bild 8 iterativ gelöst. Die Genauigkeit der numerischen Lösung hängt von der Maschenweite des Gitters, der Größe der Zeitschritte und der Wahl der Abbruchkriterien ab. In der Regel ist die numerische Lösung so genau, dass der Einfluss der numerischen Parameter gegenüber dem Einfluss der physikalischen Parameter, wie Material- und Klimadaten, vernachlässigt werden kann. Nach der Berechnung sollte eine Ergebniskontrolle durchgeführt werden, um Bedienungs- oder schwere Konvergenzfehler ausschließen zu können. Konvergenzprobleme werden von WUFI angezeigt und ihre Auswirkungen anhand eines Vergleichs der aufsummierten Feuchteströme und des akkumulierten Wassers im Bauteil ausgewertet. Falsche Eingaben oder unrealistische Materialdaten können nur durch Plausibilitätskontrollen eingegrenzt werden.
7. Praktische Schlussfolgerungen
Die rechnerische Simulation des instationären Wärme- und Feuchtetransports bietet auch für die Praxis zahlreiche Vorteile. So sind etwa die folgenden Einsatzbereiche und Aussagemöglichkeiten in Bezug auf das klimabedingte hygrothermische Bauteilverhalten zu nennen, die über die bisherigen Beurteilungsmöglichkeiten nach Glaser deutlich hinausgehen:
- reale Tauwassersituation während der Heizperiode unter Berücksichtigung von Wasserdampfsorption und Kapillarleitung
- Austrocknen von Baufeuchte
- Sommerkondensation durch Umkehrdiffusion
- solare Einstrahlung, Schlagregenbelastung und Oberflächenbetauung bei Dächern und Fassaden
- Feuchteeinfluss auf Energiehaushalt
Die Ergebnisse für Feuchte und Temperatur im Bauteil sind in beliebiger Orts- und Zeitauflösung verfügbar. Sie können beispielsweise verwendet werden zur:
- Extrapolation von Versuchsergebnissen
- Übertragung von bewährten Konstruktionen auf andere Klimaverhältnisse
- Planung von Neubau-, Umbau- und Sanierungsmaßnahmen
- Entwicklung und Optimierung von Bauprodukten
- Ermittlung von maximal zulässigen Raumluftfeuchtelasten
- Bestimmung der hygrothermischen Einsatzvoraussetzungen und Anwendungsgrenzen von Baustoffen und Bauteilen
Die aufgezeigten Vorteile der hygrothermischen Simulation haben in den letzten Jahren zu einer starken Nachfrage nach rechnerischen Untersuchungen vor allem im Bereich der Altbausanierung geführt, da dort Standardlösungen häufig versagen. Bisher fehlen jedoch allgemeingültige Richtlinien für die Leistungsbeschreibung und Anwendung der neuen Verfahren. Deshalb wurde 1997 auf Initiative der WTA (Wissenschaftlich-Technische Arbeitsgemeinschaft für Bauwerkserhaltung und Denkmalpflege) eine WTA-Arbeitsgruppe gebildet, die die Erstellung solcher Richtlinien zur Aufgabe hat. Ein ähnliches Ziel verfolgt die im Jahr 2000 gegründete Task Group "Moisture Calculation" im Rahmen des europäischen Normungsausschusses TC89 (Thermal Performance of Buildings and Building Components). Damit werden sowohl auf nationaler als auch auf internationaler Ebene die Voraussetzungen für den geregelten Einsatz von hygrothermischen Simulationsverfahren im Bauwesen geschaffen.
Literatur
[ 1] Cammerer, J. und Achtziger,J.: Einfluß des Feuchtegehaltes auf die Wärmeleitfähigkeit von Bau- und Dämmstoffen. Bericht zu BmBau Forschungsvorhaben BI 5-800883-4, 1984.
[ 2] Künzel H.M.: Verfahren zur ein- und zweidimensionalen Berechnung des gekoppelten Wärme- und Feuchtetransports in Bauteilen mit einfachen Kennwerten; Dissertation Universität Stuttgart 1994.
[ 3] Künzel, H.M. und Holm, A.: Praktische Beurteilung von Putzen durch moderne bauphysikalische Bewertung. WTA-Schriftenreihe (1999), Heft 20, S.177-132.
[ 4] Arnold, A.: Salze, lästige weiße Ausblühungen oder Hauptschadensursache. Jahresbericht Steinzerfall-Steinkonservierung 1990, Verlag Ernst & Sohn, S. 1-9.
[ 5] Sedlbauer, K. und Krus, M.: Schadensrisiko bei Ziegel-Außenbauteilen durch Niederschlag und Frosteinwirkung. Feuchtetag 1999 DGZfP-Berichtsband BB 69-CD, Vortrag U4, S.1-8.
[ 6] Krus, M.: Feuchtetransport- und Speicherkoeffizienten poröser mineralischer Baustoffe. Theoretische Grundlagen und neue Meßtechniken. Dissertation Universität Stuttgart 1995.
[ 7] Künzel, H.M.: Einfluß der Mittelwertbildung von Klimadaten auf die Ergebnisse von Feuchtetransportberechnungen. Tagungsband 9. Bauklimatisches Symposium, Dresden 1994, S. 332-344.
[ 8] Künzel, H.M. und Schmidt, Th.: Auswahl und Aufbereitung von meteorologischen Datensätzen für Feuchtetransportberechnungen. Tagungs-band 10. Bauklimatisches Symposium, Dresden 1999, S. 637-647.
[ 9] Künzel, H.M.: Raumluftfeuchteverhältnisse in Wohnräumen. IBP-Mitteilung 24 (1997) Nr. 314.
[10] Hens, H.: Modelling Heat Air and Moisture Transfer in Insulated Envelope Parts. Final Report IEA-Annex 24, KU Leuven 1996.